Search any question & find its solution
Question:
Answered & Verified by Expert
$\Pi_1, \Pi_2, \Pi_3$ are three planes which are respectively parallel to the $Y Z, Z X$ and $X Y$ planes at distances $a, b$ and $c$ forming a rectangular parallelopiped. $d_1$ is a diagonal of the face of $X Y$-plane not passing through the origin and $d_2$ is a diagonal of the plane $\Pi_2$ coterminous with $d_1$. If none of the coordinates of the vertices of the parallelopiped are negative, then the angle between $d_1$ and $d_2$ is
Options:
Solution:
1402 Upvotes
Verified Answer
The correct answer is:
$\cos ^{-1}\left(\frac{a^2}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}}\right)$
Direction ratio of diagonal $d_1$ i.e., direction of $A E$ is $a \hat{\mathbf{i}}-b \hat{\mathbf{j}}$
Direction ratio of diagonal $d_2$ i.e., direction of $A D$ $a \hat{\mathbf{i}}-c \hat{\mathbf{k}}$
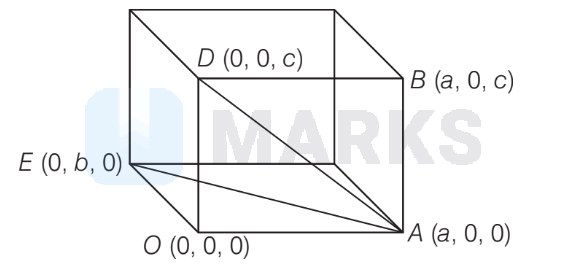
Angle between diagonal $d_1$ and diagonal $d_2$
$\begin{aligned}
\cos \theta & =\frac{(a \hat{\mathbf{i}}-b \hat{\mathbf{j}}) \cdot(a \hat{\mathbf{i}}-c \hat{\mathbf{k}})}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}}=\frac{a^2}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}} \\
\Rightarrow \quad \theta & =\cos ^{-1}\left(\frac{a^2}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}}\right)
\end{aligned}$
Direction ratio of diagonal $d_2$ i.e., direction of $A D$ $a \hat{\mathbf{i}}-c \hat{\mathbf{k}}$

Angle between diagonal $d_1$ and diagonal $d_2$
$\begin{aligned}
\cos \theta & =\frac{(a \hat{\mathbf{i}}-b \hat{\mathbf{j}}) \cdot(a \hat{\mathbf{i}}-c \hat{\mathbf{k}})}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}}=\frac{a^2}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}} \\
\Rightarrow \quad \theta & =\cos ^{-1}\left(\frac{a^2}{\sqrt{a^2+b^2} \sqrt{a^2+c^2}}\right)
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.