Search any question & find its solution
Question:
Answered & Verified by Expert
18. The sides of a rectangle are given by the equations $x=-2, x=4, y=-2$ and $y=5$
Then the equation of the circle, whose centre is the point of intersection of the diagonals, lying within the rectangle and touching only two opposite sides, is
Options:
Then the equation of the circle, whose centre is the point of intersection of the diagonals, lying within the rectangle and touching only two opposite sides, is
Solution:
2431 Upvotes
Verified Answer
The correct answer is:
$x^2+y^2-2 x-3 y-9=0$
The given equations of the sides are $x=-2$, $x=4, y=-2, y=5$
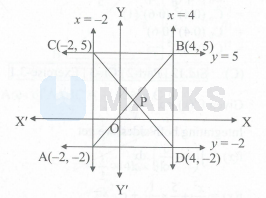
$\therefore \quad$ According to the given condition, centre of the required circle is $P$.
$\therefore \quad$ The co-ordinates of $\mathrm{P}$ are $\left(1, \frac{3}{2}\right)$.
As circle touches only 2 opposite sides, its radius is either 3.5 units or 3 units.
$\therefore \quad$ Equation of the required circle is
$\begin{aligned}
& x^2+y^2-2 x-3 y-\frac{23}{4}=0 \text { or } \\
& x^2+y^2-2 x-3 y-9=0
\end{aligned}$
$\therefore \quad$ Option (D) is correct.

$\therefore \quad$ According to the given condition, centre of the required circle is $P$.
$\therefore \quad$ The co-ordinates of $\mathrm{P}$ are $\left(1, \frac{3}{2}\right)$.
As circle touches only 2 opposite sides, its radius is either 3.5 units or 3 units.
$\therefore \quad$ Equation of the required circle is
$\begin{aligned}
& x^2+y^2-2 x-3 y-\frac{23}{4}=0 \text { or } \\
& x^2+y^2-2 x-3 y-9=0
\end{aligned}$
$\therefore \quad$ Option (D) is correct.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.