Search any question & find its solution
Question:
Answered & Verified by Expert
19.5 of \(\mathrm{CH}_2 \mathrm{FCOOH}\) is dissolved in \(500 \mathrm{~g}\) of water. The depression in the freezing point of water observed is \(1 \cdot 0^{\circ} \mathrm{C}\). Calculate the van't Hoff factor and dissociation constant of fluoroacetic acid.
Solution:
2087 Upvotes
Verified Answer
Using the relation,
\(=\frac{1000 \times 1.86 \times 19.5}{500 \times 1}=72.54 \mathrm{~g} \mathrm{~mol}^{-1}\)
\(M_2(\) Calculated \()=12+2+19+12+2 \times 16+1\)
\(=78 \mathrm{~g} \mathrm{~mol}^{-1}\)
\(\therefore i=\frac{M_2 \text { (calculated) }}{M_2 \text { (observed) }}=\frac{78}{72.54}=1.0753\).
Calculation of dissociation constant :
Let \(\alpha\) be the degree of dissociation and \(\mathrm{C}\) be the initial concentration of \(\mathrm{CH}_2 \mathrm{FCOOH}\)
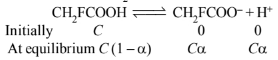
\(\begin{aligned}
&i=\frac{C(1+\alpha)}{C}=1+\alpha \\
&\alpha=i-1=1.0753-1=0.0753 \\
&K_a=\frac{C \alpha C \alpha}{C(1-\alpha)}=\frac{C \alpha^2}{1-\alpha}
\end{aligned}\)
Taking the volume of solution as \(500 \mathrm{~mL}\)
\(\begin{aligned}
&\mathrm{C}=\frac{19.5}{\frac{78}{500} \times 1000} \mathrm{M}=0.5 \mathrm{M} \\
&\therefore \quad K_a=\frac{0.5 \times(0.0753)^2}{(1-0.0753)}=3.07 \times 10^{-3}
\end{aligned}\)
\(=\frac{1000 \times 1.86 \times 19.5}{500 \times 1}=72.54 \mathrm{~g} \mathrm{~mol}^{-1}\)
\(M_2(\) Calculated \()=12+2+19+12+2 \times 16+1\)
\(=78 \mathrm{~g} \mathrm{~mol}^{-1}\)
\(\therefore i=\frac{M_2 \text { (calculated) }}{M_2 \text { (observed) }}=\frac{78}{72.54}=1.0753\).
Calculation of dissociation constant :
Let \(\alpha\) be the degree of dissociation and \(\mathrm{C}\) be the initial concentration of \(\mathrm{CH}_2 \mathrm{FCOOH}\)
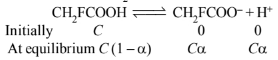
\(\begin{aligned}
&i=\frac{C(1+\alpha)}{C}=1+\alpha \\
&\alpha=i-1=1.0753-1=0.0753 \\
&K_a=\frac{C \alpha C \alpha}{C(1-\alpha)}=\frac{C \alpha^2}{1-\alpha}
\end{aligned}\)
Taking the volume of solution as \(500 \mathrm{~mL}\)
\(\begin{aligned}
&\mathrm{C}=\frac{19.5}{\frac{78}{500} \times 1000} \mathrm{M}=0.5 \mathrm{M} \\
&\therefore \quad K_a=\frac{0.5 \times(0.0753)^2}{(1-0.0753)}=3.07 \times 10^{-3}
\end{aligned}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.