Search any question & find its solution
Question:
Answered & Verified by Expert
2 aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly is 0.3 and 0.2 respectively. The second plane will bomb only if first misses the target. The probability that the target is hit by the 2 nd plane is
Options:
Solution:
1771 Upvotes
Verified Answer
The correct answer is:
$0.32$
Let $A$ be the event that aeroplane-I hit the target correctly and $B$ be the event that aeroplane-II hit the target correctly.
$\begin{array}{ll}\Rightarrow & P(A)=0.3 \text { and } P(B)=0.2 \\ \therefore & P\left(A^{\prime}\right)=1-P(A)=1-0.3=0.7\end{array}$
where $A^{\prime}$, first mises the target
$P\left(B^{\prime}\right)=1-P(B)=1-0.2=0.8$
$B^{\prime}$, second misses the target.
Let $X$ be the event that target is hit by plane-II
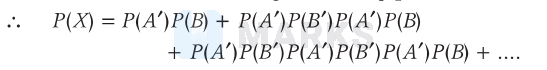
$\begin{aligned}=0.7 \times 0.2 & +0.7 \times 0.8 \times 0.7 \times 0.2 \\ & +0.7 \times 0.8 \times 0.7 \times 0.8 \times 0.7 \times 0.2+\ldots\end{aligned}$
$=0.14\left[1+(0.56)+(0.56)^2+\ldots\right]$
$=0.14\left[\frac{1}{1-0.56}\right]$
$\left[\because 1+0.56+(0.56)^2+\ldots\right.$ forms an infinite GP
whose sum $=\frac{a}{1-r}$ where $a$ is first term and $r$ is common ratio]
$=0.14 \times \frac{1}{0.44}$
$P(X)=0.32$
$\begin{array}{ll}\Rightarrow & P(A)=0.3 \text { and } P(B)=0.2 \\ \therefore & P\left(A^{\prime}\right)=1-P(A)=1-0.3=0.7\end{array}$
where $A^{\prime}$, first mises the target
$P\left(B^{\prime}\right)=1-P(B)=1-0.2=0.8$
$B^{\prime}$, second misses the target.
Let $X$ be the event that target is hit by plane-II
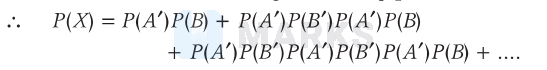
$\begin{aligned}=0.7 \times 0.2 & +0.7 \times 0.8 \times 0.7 \times 0.2 \\ & +0.7 \times 0.8 \times 0.7 \times 0.8 \times 0.7 \times 0.2+\ldots\end{aligned}$
$=0.14\left[1+(0.56)+(0.56)^2+\ldots\right]$
$=0.14\left[\frac{1}{1-0.56}\right]$
$\left[\because 1+0.56+(0.56)^2+\ldots\right.$ forms an infinite GP
whose sum $=\frac{a}{1-r}$ where $a$ is first term and $r$ is common ratio]
$=0.14 \times \frac{1}{0.44}$
$P(X)=0.32$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.