Search any question & find its solution
Question:
Answered & Verified by Expert
$25.3 \mathrm{~g}$ of sodium carbonate, $\mathrm{Na}_2 \mathrm{CO}_3$ is dissolved in enough water to make $250 \mathrm{~mL}$ of solution. If sodium carbonate dissociates completely, molar concentration of sodium ion, $\mathrm{Na}^{+}$and carbonate ion, $\mathrm{CO}_3^{2-}$ are respectively (Molar mass of $\mathrm{Na}_2 \mathrm{CO}_3=106 \mathrm{~g} \mathrm{~mol}^{-1}$ )
Options:
Solution:
1269 Upvotes
Verified Answer
The correct answer is:
$1.910 \mathrm{M}$ and $0.955 \mathrm{M}$
$$
\begin{aligned}
\text { Molarity } & =\frac{\text { number of moles of solute }}{\text { volume of solution (in mL) }} \times 1000 \\
& =\frac{25.3 \times 1000}{106 \times 250}=0.9547 \approx 0.955 \mathrm{M}
\end{aligned}
$$
$\mathrm{Na}_2 \mathrm{CO}_3$ in aqueous solution remains dissociated as
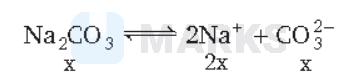
Since, the molarity of $\mathrm{Na}_2 \mathrm{CO}_3$ is $0.955 \mathrm{M}$, the molarity of $\mathrm{CO}_3^{2-}$ is also $0.955 \mathrm{M}$ and that of $\mathrm{Na}^{+}$is $2 \times 0.955=1.910 \mathrm{M}$
\begin{aligned}
\text { Molarity } & =\frac{\text { number of moles of solute }}{\text { volume of solution (in mL) }} \times 1000 \\
& =\frac{25.3 \times 1000}{106 \times 250}=0.9547 \approx 0.955 \mathrm{M}
\end{aligned}
$$
$\mathrm{Na}_2 \mathrm{CO}_3$ in aqueous solution remains dissociated as
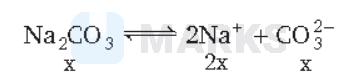
Since, the molarity of $\mathrm{Na}_2 \mathrm{CO}_3$ is $0.955 \mathrm{M}$, the molarity of $\mathrm{CO}_3^{2-}$ is also $0.955 \mathrm{M}$ and that of $\mathrm{Na}^{+}$is $2 \times 0.955=1.910 \mathrm{M}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.