Search any question & find its solution
Question:
Answered & Verified by Expert
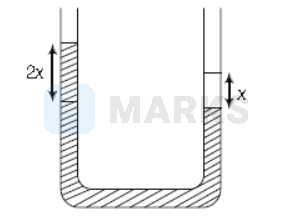
$9 \mathrm{~kg}$ solution is poured into a glass U-tube as shown in the figure below. The tube's inner diameter is $2 \sqrt{\frac{\pi}{5}} \mathrm{~m}$ and the solution oscillates freely up and down about its position of equilibriwm $(x=0)$. The period of oscillation in seconds is $\left(1 \mathrm{~m}^3\right.$ of solution has a mass $\mu=900 \mathrm{~kg}, g=10 \mathrm{~m} / \mathrm{s}^2$, ignore frictional and swrface tension effects)
Options:

Solution:
2565 Upvotes
Verified Answer
The correct answer is:
0.1
Diameter of tube $=2 \sqrt{\frac{\pi}{5}} \mathrm{~m}$
$\therefore$ Radius of tube $(r)=\sqrt{\frac{\pi}{5}} \mathrm{~m}$
Mass of solution $(u)=9 \mathrm{~kg}$
We know that,
$$
\begin{aligned}
& \because \quad \operatorname{Mass}(u)=d \cdot v \\
& \therefore \quad u=d \pi r^2 L \\
&
\end{aligned}
$$
or,
$$
9=900 \times \pi \times\left(\sqrt{\frac{\pi}{5}}\right)^2 L
$$
or,
$$
9=900 \times \frac{\pi^2}{5} \times 1
$$
or,
$L=\frac{5}{100 \pi^2}$
Now, $\quad T=2 \pi \sqrt{\frac{L}{2 g}}$
From Eq. (i),
Or,
$$
\begin{aligned}
& T=2 \pi \sqrt{\frac{5}{200 \pi^2 \times 10}} \\
& T=2 \times \sqrt{\frac{1}{400}}=\frac{2}{20} \\
& T=0.1 \mathrm{~s}
\end{aligned}
$$
$\therefore$ Radius of tube $(r)=\sqrt{\frac{\pi}{5}} \mathrm{~m}$
Mass of solution $(u)=9 \mathrm{~kg}$
We know that,
$$
\begin{aligned}
& \because \quad \operatorname{Mass}(u)=d \cdot v \\
& \therefore \quad u=d \pi r^2 L \\
&
\end{aligned}
$$
or,
$$
9=900 \times \pi \times\left(\sqrt{\frac{\pi}{5}}\right)^2 L
$$
or,
$$
9=900 \times \frac{\pi^2}{5} \times 1
$$
or,
$L=\frac{5}{100 \pi^2}$
Now, $\quad T=2 \pi \sqrt{\frac{L}{2 g}}$
From Eq. (i),
Or,
$$
\begin{aligned}
& T=2 \pi \sqrt{\frac{5}{200 \pi^2 \times 10}} \\
& T=2 \times \sqrt{\frac{1}{400}}=\frac{2}{20} \\
& T=0.1 \mathrm{~s}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.