Search any question & find its solution
Question:
Answered & Verified by Expert
$\mathrm{A}(1,15), \mathrm{B}(3,-12), \mathrm{C}(6,12)$ are three consecutive turning points of a continuous curve $y=f(x)$. If $f(x)=0$ only for $x=\alpha$ and $x=\beta$, then $|\beta-\alpha| < $
Options:
Solution:
1123 Upvotes
Verified Answer
The correct answer is:
$5$
Given that $\mathrm{A}(1,15), \mathrm{B}(3,-12), \mathrm{C}(6,12)$ are threeconsecutive turning points of continuous curve $y=f(x)$ and intersect $x$-axis at $x=\alpha$, and $x=\beta$.
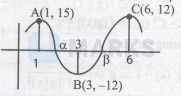
It is clear from graph is
$\begin{aligned}
& 1 < \alpha < 3 \text { and } 3 < \beta < 6 \Rightarrow-\alpha < -1 \text { and } \beta < 6 \\
& \Rightarrow|\beta-\alpha| < 6-1 \Rightarrow|\beta-\alpha| < 5 .
\end{aligned}$

It is clear from graph is
$\begin{aligned}
& 1 < \alpha < 3 \text { and } 3 < \beta < 6 \Rightarrow-\alpha < -1 \text { and } \beta < 6 \\
& \Rightarrow|\beta-\alpha| < 6-1 \Rightarrow|\beta-\alpha| < 5 .
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.