Search any question & find its solution
Question:
Answered & Verified by Expert
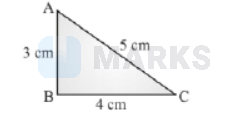
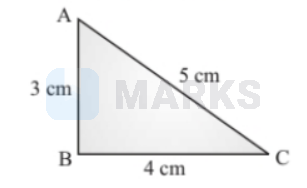
A $12 \mathrm{~cm}$ wire is given a shape of a right angled triangle $A B C$ having sides $3 \mathrm{~cm}$, $4 \mathrm{~cm}$ and $5 \mathrm{~cm}$ as shown in the figure. The resistance between two ends (AB, $B C, C A)$ of the respective sides are measured one by one by a multi-meter. The resistance will be in the ratio:
Options:

Solution:
2746 Upvotes
Verified Answer
The correct answer is:
$27: 32: 35$
Resistance of side $A B=R_1=\frac{3 \rho}{A}$
Resistance of side $B C=R_2=\frac{4 \rho}{A}$
Resistance of side $\mathrm{AC}=\mathrm{P}_3=\frac{5 \rho}{\mathrm{A}}$
(Where $A=$ Area of cross-section and $\rho=$ resistivity of wire)
$\therefore$ The resistance between $\mathrm{A}$ and $\mathrm{B}$ is
$$
\begin{aligned}
& \mathrm{R}_{\mathrm{AB}}=\frac{R_1\left(R_2+R_3\right)}{R_1+R_2+R_3}=\frac{\frac{3 \rho}{A}\left(\frac{4 \rho}{A}+\frac{5 \rho}{A}\right)}{\frac{3 \rho}{A}+\frac{4 \rho}{A}+\frac{5 \rho}{A}} \\
& =\frac{27 \rho}{12 A} \\
& \text { Similarly } R_{B C}=\frac{R_2\left(R_1+R_3\right)}{R_1+R_2+R_3} \\
& \frac{\frac{4 \rho}{A}\left(\frac{3 \rho}{A}+\frac{5 \rho}{A}\right)}{\frac{3 \rho}{A}+\frac{4 \rho}{A}+\frac{5 \rho}{A}}=\frac{32}{12} \frac{\rho}{A} \\
& \text { And } R_{A C}=\frac{R_3\left(R_1+R_2\right)}{R_1+R_2+R_3} \\
& =\frac{\frac{5 \rho}{A}\left(\frac{3 \rho}{A}+\frac{3 \rho}{A}\right)}{\frac{5 \rho}{A}+\frac{3 \rho}{A}+\frac{4 \rho}{A}}=\frac{35}{12} \frac{\rho}{A} \\
& \therefore R_{A B}: R_{B C}: R_{A C}=\frac{27}{12}: \frac{32}{12}: \frac{35}{12} \\
& =27: 32: 35 \\
&
\end{aligned}
$$
Resistance of side $B C=R_2=\frac{4 \rho}{A}$
Resistance of side $\mathrm{AC}=\mathrm{P}_3=\frac{5 \rho}{\mathrm{A}}$
(Where $A=$ Area of cross-section and $\rho=$ resistivity of wire)

$\therefore$ The resistance between $\mathrm{A}$ and $\mathrm{B}$ is
$$
\begin{aligned}
& \mathrm{R}_{\mathrm{AB}}=\frac{R_1\left(R_2+R_3\right)}{R_1+R_2+R_3}=\frac{\frac{3 \rho}{A}\left(\frac{4 \rho}{A}+\frac{5 \rho}{A}\right)}{\frac{3 \rho}{A}+\frac{4 \rho}{A}+\frac{5 \rho}{A}} \\
& =\frac{27 \rho}{12 A} \\
& \text { Similarly } R_{B C}=\frac{R_2\left(R_1+R_3\right)}{R_1+R_2+R_3} \\
& \frac{\frac{4 \rho}{A}\left(\frac{3 \rho}{A}+\frac{5 \rho}{A}\right)}{\frac{3 \rho}{A}+\frac{4 \rho}{A}+\frac{5 \rho}{A}}=\frac{32}{12} \frac{\rho}{A} \\
& \text { And } R_{A C}=\frac{R_3\left(R_1+R_2\right)}{R_1+R_2+R_3} \\
& =\frac{\frac{5 \rho}{A}\left(\frac{3 \rho}{A}+\frac{3 \rho}{A}\right)}{\frac{5 \rho}{A}+\frac{3 \rho}{A}+\frac{4 \rho}{A}}=\frac{35}{12} \frac{\rho}{A} \\
& \therefore R_{A B}: R_{B C}: R_{A C}=\frac{27}{12}: \frac{32}{12}: \frac{35}{12} \\
& =27: 32: 35 \\
&
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.