Search any question & find its solution
Question:
Answered & Verified by Expert
A $12.5 \mathrm{eV}$ electron beam is used to bombard gaseous hydrogen at room temperature. It will emit:
Options:
Solution:
2684 Upvotes
Verified Answer
The correct answer is:
2 lines in the Lyman series and 1 line in the Balmar series
2 lines in the Lyman series and 1 line in the Balmar series
$$
\begin{aligned}
&\mathrm{E}=\frac{\mathrm{hc}}{\lambda} \Rightarrow \lambda=\frac{\mathrm{hc}}{\mathrm{E}}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{12.5 \times 1.6 \times 10^{-19}} \\
&=993 \mathrm{~A}^{\circ} \\
&\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right) \\
&
\end{aligned}
$$
(where Rydberg constant , $\mathrm{R}=1.097 \times 10^7$ )
or, $\frac{1}{993 \times 10^{-10}}=1.097 \times 10^7\left(\frac{1}{1^2}-\frac{1}{\mathrm{n}_2^2}\right)$
Solving we get $\mathrm{n}_2=3$
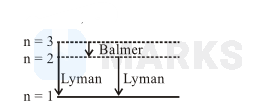
Spectral lines
Total number of spectral lines $=3$
Two lines in Lyman series for $\mathrm{n}_1=1, \mathrm{n}_2=2$ and $\mathrm{n}_1=1, \mathrm{n}_2=3$ and one in Balmer series for $\mathrm{n}_1=2, \mathrm{n}_2=3$
\begin{aligned}
&\mathrm{E}=\frac{\mathrm{hc}}{\lambda} \Rightarrow \lambda=\frac{\mathrm{hc}}{\mathrm{E}}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{12.5 \times 1.6 \times 10^{-19}} \\
&=993 \mathrm{~A}^{\circ} \\
&\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right) \\
&
\end{aligned}
$$
(where Rydberg constant , $\mathrm{R}=1.097 \times 10^7$ )
or, $\frac{1}{993 \times 10^{-10}}=1.097 \times 10^7\left(\frac{1}{1^2}-\frac{1}{\mathrm{n}_2^2}\right)$
Solving we get $\mathrm{n}_2=3$
Spectral lines
Total number of spectral lines $=3$
Two lines in Lyman series for $\mathrm{n}_1=1, \mathrm{n}_2=2$ and $\mathrm{n}_1=1, \mathrm{n}_2=3$ and one in Balmer series for $\mathrm{n}_1=2, \mathrm{n}_2=3$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.