Search any question & find its solution
Question:
Answered & Verified by Expert
A $2 \mathrm{~m}$ wide truck is moving with a uniform speed $v_{0}=8 \mathrm{~m} / \mathrm{s}$ along a straight horizontal road. $\mathrm{A}$ pedestrain starts to cross the road with a uniform speed $v$ when the truck is 4 m away from him. The minimum value of $v$ so that he can cross the road safely is
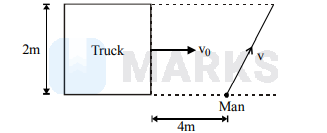
Options:

Solution:
2641 Upvotes
Verified Answer
The correct answer is:
$3.57 \mathrm{~m} / \mathrm{s}$
Let the man starts crossing the road at an angle $\theta$ as shown in figure. For safe crossing the condition is that the man must cross the road by the time the truck describes the distance 4 । $A C$ or 4 । $2 \cot \theta$. $\therefore \frac{4+2 \cot \theta}{8}=\frac{2 / \sin \theta}{v}$ or $v=\frac{8}{2 \sin \theta+\cos \theta}$
For minimum $v, \frac{d v}{d \theta}=0$
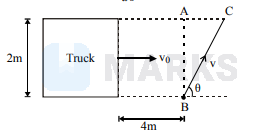
or $\frac{-8(2 \cos \theta-\sin \theta)}{(2 \sin \theta+\cos \theta)^{2}}=0$ or $2 \cos \theta-$
$\sin \theta=0$
or $\tan \theta=2$
From equation (i),
$$
v_{\min }=\frac{8}{2\left(\frac{2}{\sqrt{5}}\right)+\frac{1}{\sqrt{5}}}=\frac{8}{\sqrt{5}}=3.57 \mathrm{~m} / \mathrm{s}
$$
For minimum $v, \frac{d v}{d \theta}=0$

or $\frac{-8(2 \cos \theta-\sin \theta)}{(2 \sin \theta+\cos \theta)^{2}}=0$ or $2 \cos \theta-$
$\sin \theta=0$
or $\tan \theta=2$
From equation (i),
$$
v_{\min }=\frac{8}{2\left(\frac{2}{\sqrt{5}}\right)+\frac{1}{\sqrt{5}}}=\frac{8}{\sqrt{5}}=3.57 \mathrm{~m} / \mathrm{s}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.