Search any question & find its solution
Question:
Answered & Verified by Expert
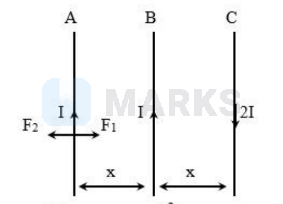
$\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three parallel conductors of equal lengths carrying currents I, I and 2I respectively. Distance between A and $B$ is ' $x$ ' and that between B and $C$ is also ' $x$ '. $F_1$ is the force exerted by conductor $\mathrm{B}$ on $\mathrm{A}$. $\mathrm{F}_2$ is the force exerted by conductor $\mathrm{C}$ on $\mathrm{A}$. Current $\mathrm{I}$ in $\mathrm{A}$ and $\mathrm{I}$ in $\mathrm{B}$ are in same direction and current $2 \mathrm{I}$ in $\mathrm{C}$ is in opposite direction. Then
Options:
Solution:
1480 Upvotes
Verified Answer
The correct answer is:
$\mathrm{F}_1=-\mathrm{F}_2$
Current in A and B are in the same direction. Hence force $F_1$ exerted by B on A will be attractive (towards B). Current in A and $\mathrm{C}$ are in opposite directions. Hence force $\mathrm{F}_2$, exerted by $\mathrm{C}$ on A will be repulsive (away from $C$ ). Thus $F_1$ and $F_2$ are opposite in direction.
$$
\begin{aligned}
& \mathrm{F}_1=\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}_1 \mathrm{I}_2}{\mathrm{x}} \cdot \mathrm{L}=\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}^2}{\mathrm{x}} \mathrm{L} \\
& \mathrm{F}_2=\frac{\mu_0}{2 \pi} \cdot \frac{2 \mathrm{I}^2}{2 \mathrm{x}} \cdot \mathrm{L}=\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}^2}{\mathrm{x}} \cdot \mathrm{L}
\end{aligned}
$$
$\therefore \mathrm{F}_1$ and $\mathrm{F}_2$ have some magnitude.
$$
\therefore \mathrm{F}_1=-\mathrm{F}_2
$$

$$
\begin{aligned}
& \mathrm{F}_1=\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}_1 \mathrm{I}_2}{\mathrm{x}} \cdot \mathrm{L}=\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}^2}{\mathrm{x}} \mathrm{L} \\
& \mathrm{F}_2=\frac{\mu_0}{2 \pi} \cdot \frac{2 \mathrm{I}^2}{2 \mathrm{x}} \cdot \mathrm{L}=\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}^2}{\mathrm{x}} \cdot \mathrm{L}
\end{aligned}
$$
$\therefore \mathrm{F}_1$ and $\mathrm{F}_2$ have some magnitude.
$$
\therefore \mathrm{F}_1=-\mathrm{F}_2
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.