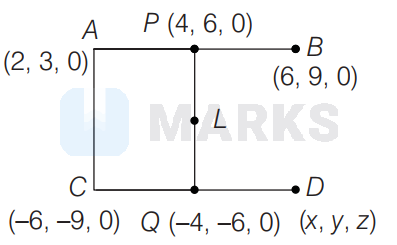
Let coordinate of $D$ is $(x, y, z)$.
Using mid-point formula,
$$
\begin{aligned}
Q &=\left(\frac{x-6}{2}, \frac{y-9}{2}, \frac{z+0}{2}\right) \\
\text { Also, } \quad P &=\left(\frac{2+6}{2}, \frac{3+9}{2}, \frac{0+0}{2}\right)=(4,6,0)
\end{aligned}
$$
Since, $A C \| P Q$
$$
\begin{aligned}
&\therefore \text { D.R'.s of line } A C=\text { D.R' s of line } P Q \\
&\Rightarrow(-8,-12,0)=\left(\frac{x-14}{2}, \frac{y-21}{2}, \frac{z}{2}\right) \\
&\Rightarrow x=-2, y=-3, z=0 \\
&\Rightarrow D(-2,-3,0) \Rightarrow Q(-4,-6,0)
\end{aligned}
$$
If $L$ is mid-point of $P Q$, then
$$
L\left(\frac{4-4}{2}, \frac{6-6}{2}, 0\right)=(0,0,0)
$$
$\therefore$ Perpendicular distance of $L(0,0,0)$ from the plane $3 x+4 z+25=0$ is
$$
\left|\frac{3(0)+4(0)+25}{\sqrt{(3)^{2}+(4)^{2}}}\right|=\left|\frac{25}{\sqrt{25}}\right|=\sqrt{25}=5
$$