Search any question & find its solution
Question:
Answered & Verified by Expert
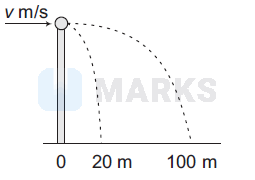
A ball of mass $0.2 \mathrm{~kg}$ rests on a vertical post of height $5 \mathrm{~m}$. A bullet of mass $0.01 \mathrm{~kg}$, travelling with a velocity $v \mathrm{~m} / \mathrm{s}$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $20 \mathrm{~m}$ and the bullet at a distance of $100 \mathrm{~m}$ from the foot of the post. The initial velocity $v$ of the bullet is
Options:

Solution:
1004 Upvotes
Verified Answer
The correct answer is:
$500 \mathrm{~m} / \mathrm{s}$
$500 \mathrm{~m} / \mathrm{s}$
Time taken by the bullet and ball to strike the ground is
$$
t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 5}{10}}=1 \mathrm{~s}
$$
Let $v_1$ and $v_2$ are the velocities of ball and bullet after collision.
Then applying
We have, $20=v_1 \times 1$
or $v_1=20 \mathrm{~ms}^{-1}$
$$
100=v_2 \times 1 \text { or } v_2=100 \mathrm{~m} / \mathrm{s}^{-1}
$$
Now, from conservation of linear momentum before and after collision we have,
$0.01 v=(0.2 \times 20)+(0.01 \times 100)$
On solving, we get
$$
v=500 \mathrm{~ms}^{-1}
$$
$\therefore$ Correct answer is (d).
Analysis of Question
Question is moderately lengthy from calculation point of view, otherwise it is simple.
$$
t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 5}{10}}=1 \mathrm{~s}
$$
Let $v_1$ and $v_2$ are the velocities of ball and bullet after collision.
Then applying
We have, $20=v_1 \times 1$
or $v_1=20 \mathrm{~ms}^{-1}$
$$
100=v_2 \times 1 \text { or } v_2=100 \mathrm{~m} / \mathrm{s}^{-1}
$$
Now, from conservation of linear momentum before and after collision we have,
$0.01 v=(0.2 \times 20)+(0.01 \times 100)$
On solving, we get
$$
v=500 \mathrm{~ms}^{-1}
$$
$\therefore$ Correct answer is (d).
Analysis of Question
Question is moderately lengthy from calculation point of view, otherwise it is simple.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.