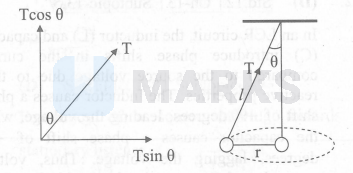
The tension in the string can be resolved in two components along the perpendicular axis. The gravitational force is acting downwards and the centrifugal force is acting in $-\mathrm{x}$ direction
$$
\begin{aligned}
& \mathrm{T} \sin \theta=\mathrm{mr} \omega^2 \\
\therefore \quad & \omega^2=\frac{\mathrm{T} \sin \theta}{\mathrm{mr}}
\end{aligned}
$$
$$
\therefore \quad \omega=\sqrt{\frac{\mathrm{T} \sin \theta}{\mathrm{mr}}}
$$

From figure, $\sin \theta=\frac{\mathrm{r}}{l}$
$$
\begin{aligned}
& \therefore \quad \omega=\sqrt{\frac{\mathrm{Tr}}{\mathrm{mr} l}} \\
& \therefore \quad \omega=\sqrt{\frac{\mathrm{T}}{\mathrm{m} l}} \\
&
\end{aligned}
$$