Search any question & find its solution
Question:
Answered & Verified by Expert
A block of mass $m$ is pulled along a horizontal surface by applying a force at an angle $\theta$ with the horizontal. If the block travels with a uniform velocity and has a displacement $d$ and the coefficient of friction is $\mu$, then the work done by the applied force is
Options:
Solution:
1309 Upvotes
Verified Answer
The correct answer is:
$\frac{\mu m g d \cos \theta}{\cos \theta+\mu \sin \theta}$
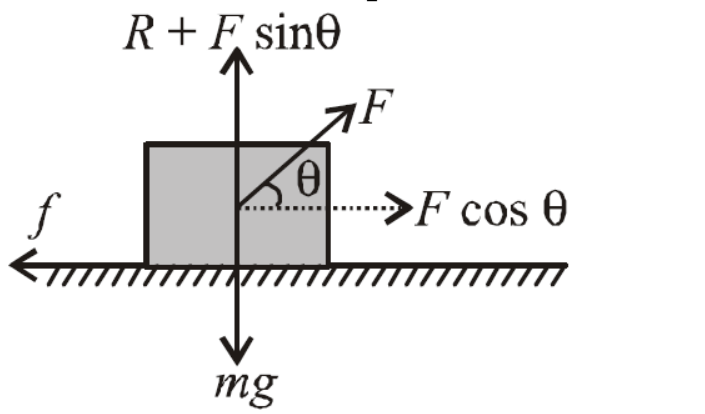
Because the block moves with a uniform velocity, the resultant force is zero. Resolving $F$ into horizontal component $F \cos \theta$ and vertical component $F \sin \theta$, we get
$$
\begin{aligned}
& R+F \sin \theta=m g \text { or } R=m g-F \sin \theta \\
& \text { Also } f=\mu R=\mu(m g-F \sin \theta) \\
& \text { But } F \cos \theta=f \\
& \text { or } F \cos \theta=\mu(m g-F \sin \theta) \\
& \text { or } F(\cos \theta+\mu \sin \theta)=\mu m g \\
& \therefore \quad F=\frac{\mu m g}{\cos \theta+\mu \sin \theta}
\end{aligned}
$$
Work $W=F s \cos \theta$
$$
\begin{aligned}
& \therefore W=\frac{\mu m g d \cos \theta}{\cos \theta+\mu \sin \theta} \\
& (\because s=d)
\end{aligned}
$$

$$
\begin{aligned}
& R+F \sin \theta=m g \text { or } R=m g-F \sin \theta \\
& \text { Also } f=\mu R=\mu(m g-F \sin \theta) \\
& \text { But } F \cos \theta=f \\
& \text { or } F \cos \theta=\mu(m g-F \sin \theta) \\
& \text { or } F(\cos \theta+\mu \sin \theta)=\mu m g \\
& \therefore \quad F=\frac{\mu m g}{\cos \theta+\mu \sin \theta}
\end{aligned}
$$
Work $W=F s \cos \theta$
$$
\begin{aligned}
& \therefore W=\frac{\mu m g d \cos \theta}{\cos \theta+\mu \sin \theta} \\
& (\because s=d)
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.