Search any question & find its solution
Question:
Answered & Verified by Expert
A body is projected at $t=0$ with a velocity $10 \mathrm{~ms}^{-1}$ at an angle of $60^{\circ}$ with the horizontal. The radius of curvature of its trajectory at $t=1$ s is $R$. Neglecting air resistance and taking acceleration due to gravity $\mathrm{g}=10 \mathrm{~ms}^{-2}$, the value of $R$ is:
Options:
Solution:
2046 Upvotes
Verified Answer
The correct answer is:
$2.8 \mathrm{~m}$
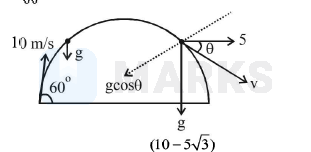
Horizontal component of velocity $\mathrm{v}_{x}=10 \cos 60^{\circ}=5 \mathrm{~m} / \mathrm{s}$
vertical component of velocity $v_{y}=10 \cos 30^{\circ}=5 \sqrt{3} \mathrm{~m} / \mathrm{s}$
After $\mathrm{t}=1 \mathrm{sec}$
Horizontal component of velocity $\mathrm{v}_{x}=5 \mathrm{~m} / \mathrm{s}$ Vertical component of velocity $v_{y}=|(5 \sqrt{3}-10)| \mathrm{m} / \mathrm{s}=10-5 \sqrt{3}$
Centripetal, acceleration $\mathrm{a}_{\mathrm{n}}=\frac{\mathrm{v}^{2}}{\mathrm{R}}$
$\Rightarrow \mathrm{R}=\frac{\mathrm{v}_{\mathrm{x}}^{2}+\mathrm{v}_{\mathrm{y}}^{2}}{\mathrm{a}_{\mathrm{n}}}=\frac{25+100+75-100 \sqrt{3}}{10 \cos \theta}$
From figure (using (i)) $\tan \theta=\frac{10-5 \sqrt{3}}{5}=2-\sqrt{3} \Rightarrow \theta=15^{\circ}$
$\mathrm{R}=\frac{100(2-\sqrt{3})}{10 \cos 15}=2.8 \mathrm{~m}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.