Search any question & find its solution
Question:
Answered & Verified by Expert
A body mass of $1 \mathrm{~kg}$, initially at rest explodes and breaks into three parts. The masses of the parts are in the ratio $1: 1: 3$. The two pieces of equal mass fly off perpendicular to each other with a speed of $30 \mathrm{~m} / \mathrm{s}$ each. The velocity of the heavier part in $\mathrm{m} / \mathrm{s}$ is
Options:
Solution:
1762 Upvotes
Verified Answer
The correct answer is:
$10 \sqrt{2}$
Initial momentum before explosion is zero. Final momentum after explosion.
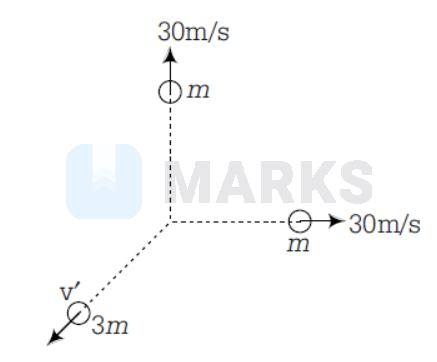
$$
\sqrt{2} \frac{m}{4} \times 30-\frac{3 m}{4} v^{\prime}
$$
From conservation of momentum
Initial momentum $=$ Final momentum
$$
\begin{aligned}
\Rightarrow \quad \sqrt{2} \frac{m}{4} \times 30-\frac{3 m}{4} v^{\prime} & =0 \\
\Rightarrow \quad v^{\prime} & =10 \sqrt{2} \mathrm{~m} / \mathrm{s}
\end{aligned}
$$

$$
\sqrt{2} \frac{m}{4} \times 30-\frac{3 m}{4} v^{\prime}
$$
From conservation of momentum
Initial momentum $=$ Final momentum
$$
\begin{aligned}
\Rightarrow \quad \sqrt{2} \frac{m}{4} \times 30-\frac{3 m}{4} v^{\prime} & =0 \\
\Rightarrow \quad v^{\prime} & =10 \sqrt{2} \mathrm{~m} / \mathrm{s}
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.