Search any question & find its solution
Question:
Answered & Verified by Expert
A body of mass $m$ is kept on a rough horizontal surface (coefficient of friction $=\mu$ ). Horizontal force is applied on the body, but it does not move. The resultant of normal reaction and the frictional force acting on the object is given $\mathrm{F}$, where $\mathrm{F}$ is
Options:
Solution:
2750 Upvotes
Verified Answer
The correct answer is:
$|\mathrm{F}| \leq m g \sqrt{1+\mu^2}$
$$
\text { The situation can be drawn as }
$$
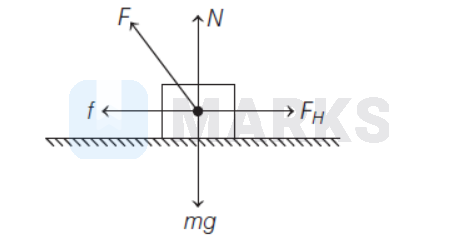
The frictional force, $\mathrm{f}=\mu \mathrm{N}=\mu \mathrm{mg} \quad[\because \mathrm{N}=\mathrm{mg}]$ From Free body diagram (FBD), the resultant force is
$$
\begin{aligned}
|F| & =\sqrt{\mathrm{N}^2+\mathrm{f}^2} \\
& =\sqrt{(\mathrm{mg})^2+(\mu \mathrm{mg})^2}=\mathrm{mg} \sqrt{1+\mu^2}
\end{aligned}
$$
This is the minimum force required to move the object. But as the body is not moving
$$
\therefore \quad|\mathrm{F}| \leq \mathrm{mg} \sqrt{1-\mu^2}
$$
\text { The situation can be drawn as }
$$

The frictional force, $\mathrm{f}=\mu \mathrm{N}=\mu \mathrm{mg} \quad[\because \mathrm{N}=\mathrm{mg}]$ From Free body diagram (FBD), the resultant force is
$$
\begin{aligned}
|F| & =\sqrt{\mathrm{N}^2+\mathrm{f}^2} \\
& =\sqrt{(\mathrm{mg})^2+(\mu \mathrm{mg})^2}=\mathrm{mg} \sqrt{1+\mu^2}
\end{aligned}
$$
This is the minimum force required to move the object. But as the body is not moving
$$
\therefore \quad|\mathrm{F}| \leq \mathrm{mg} \sqrt{1-\mu^2}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.