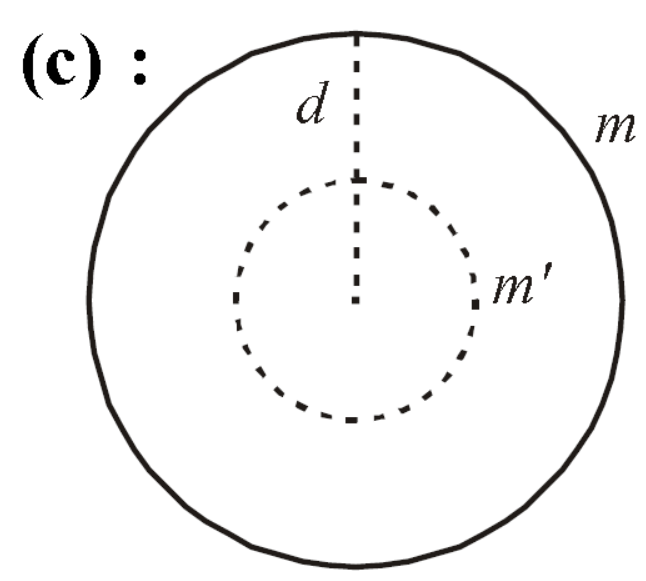
At a depth $d$ below the surface of the earth,
$$
\begin{aligned}
& m g^{\prime}=G \frac{M^{\prime} m}{(R-d)^2} \\
& M^{\prime}=\frac{4}{3} \pi(R-d)^3 \rho
\end{aligned}
$$

$$
\begin{aligned}
\Rightarrow \quad g^{\prime} & =\frac{G M^{\prime}}{(R-d)^2} \\
& =\frac{4}{3} G \pi(R-d) \rho
\end{aligned}
$$
If $\quad d=\frac{R}{2}$ then
$$
g^{\prime}=\frac{4}{3} G \pi \rho=\frac{2 \pi G R \rho}{3}
$$
On the surface of the earth
$$
\begin{aligned}
g & =\frac{G m}{R V}=\frac{4}{3} \pi G R \rho \\
\therefore \quad g^{\prime} & =\frac{g}{2}
\end{aligned}
$$

$\therefore$ The body weighed $250 \mathrm{~N}$ on the surface of the earth would weigh $\frac{1}{2} \times 250=125 \mathrm{~N}$, half way down towards the centre of the earth.