Search any question & find its solution
Question:
Answered & Verified by Expert
A body weighing $20 \mathrm{~kg}$ just slides down a rough inclined plane that rises 5 in 12 . The coefficient of friction is
Options:
Solution:
1623 Upvotes
Verified Answer
The correct answer is:
$0.46$
The given situation can be shown as
As the plane rises 5 in 12
$$
\therefore \quad \sin \theta=\frac{5}{12}
$$
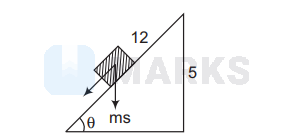
and $\cos \theta=\sqrt{1-\sin ^{2} \theta}=\sqrt{1+\left(\frac{5}{12}\right)^{2}}$
$$
=\frac{\sqrt{119}}{12}
$$
So, the coefficient of friction,
$$
\mu=\tan \theta=\frac{\sin \theta}{\cos \theta}=\frac{5}{12} \times \frac{12}{\sqrt{119}}=\frac{5}{\sqrt{119}}=0.46
$$
As the plane rises 5 in 12
$$
\therefore \quad \sin \theta=\frac{5}{12}
$$

and $\cos \theta=\sqrt{1-\sin ^{2} \theta}=\sqrt{1+\left(\frac{5}{12}\right)^{2}}$
$$
=\frac{\sqrt{119}}{12}
$$
So, the coefficient of friction,
$$
\mu=\tan \theta=\frac{\sin \theta}{\cos \theta}=\frac{5}{12} \times \frac{12}{\sqrt{119}}=\frac{5}{\sqrt{119}}=0.46
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.