Search any question & find its solution
Question:
Answered & Verified by Expert
A boy throws a ball in air at $60^{\circ}$ to the horizontal along a road with a speed of $10 \mathrm{~m} / \mathrm{s}(36 \mathrm{~km} / \mathrm{h})$. Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of $(18 \mathrm{~km} / \mathrm{h})$. Give explanation to support your diagram.
Solution:
1706 Upvotes
Verified Answer
Draw the diagram.
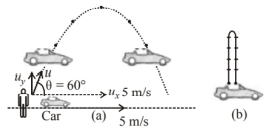
As given that, $u=\frac{36 \times 5}{18} \mathrm{~m} / \mathrm{s}=10 \mathrm{~m} / \mathrm{s}$
The boy throws the ball at an angle of $60^{\circ}$.
So, horizontal component of velocity
$$
\begin{aligned}
\left(u_x\right) &=u \cos \theta \\
&=(10 \mathrm{~m} / \mathrm{s}) \cos 60^{\circ}=10 \times \frac{1}{2}=5 \mathrm{~m} / \mathrm{sec} .
\end{aligned}
$$
Speed of the car in the direction of motion of ball
$$
=18 \mathrm{~km} / \mathrm{h}=\left(18 \times \frac{5}{18}\right)=5 \mathrm{~m} / \mathrm{sec} \text {. }
$$
As horizontal speed of ball and car is same, hence relative velocity of car and ball in the horizontal direction will be zero.
Only vertical motion of the ball will be seen by the boy in the car, as shown in fig. (b).
So vertical component of velocity,
$$
v_y=u \cos 30^{\circ}=10 \times \frac{\sqrt{3}}{2}=5 \sqrt{3} \mathrm{~m} / \mathrm{s} \text {. }
$$

As given that, $u=\frac{36 \times 5}{18} \mathrm{~m} / \mathrm{s}=10 \mathrm{~m} / \mathrm{s}$
The boy throws the ball at an angle of $60^{\circ}$.
So, horizontal component of velocity
$$
\begin{aligned}
\left(u_x\right) &=u \cos \theta \\
&=(10 \mathrm{~m} / \mathrm{s}) \cos 60^{\circ}=10 \times \frac{1}{2}=5 \mathrm{~m} / \mathrm{sec} .
\end{aligned}
$$
Speed of the car in the direction of motion of ball
$$
=18 \mathrm{~km} / \mathrm{h}=\left(18 \times \frac{5}{18}\right)=5 \mathrm{~m} / \mathrm{sec} \text {. }
$$
As horizontal speed of ball and car is same, hence relative velocity of car and ball in the horizontal direction will be zero.
Only vertical motion of the ball will be seen by the boy in the car, as shown in fig. (b).
So vertical component of velocity,
$$
v_y=u \cos 30^{\circ}=10 \times \frac{\sqrt{3}}{2}=5 \sqrt{3} \mathrm{~m} / \mathrm{s} \text {. }
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.