Search any question & find its solution
Question:
Answered & Verified by Expert
A bullet of mass $0.02 \mathrm{~kg}$ travelling horizontally with velodity $250 \mathrm{~ms}^{1}$ strikes a block of wood of mass $0.23 \mathrm{~kg}$ which rests on a rough horizontal surface. After the impact, the block and bullet move together and come to rest after travelling a distance of $40 \mathrm{~m}$. The coefficient of sliding friction of the rough surface is $\left(\mathrm{g}=9.8 \mathrm{~ms}^{-2}\right)$
Options:
Solution:
2852 Upvotes
Verified Answer
The correct answer is:
$0.51$
After collision the bullet and block move together and comes to rest after covering a distance of $40 \mathrm{~m}$.
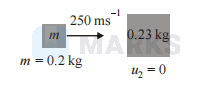
By conservation of momentum
$$
\begin{array}{l}
m_{1} u_{1}+m_{2} u_{2}=m_{1} v_{1}+m_{2} v_{2} \\
\Rightarrow 0.02 \times 250+0.23 \times 0=0.02 v+0.23 v \\
5+0=v(0.25) \text { or } v=20 \mathrm{~ms}^{-1}
\end{array}
$$
Now, by conservation of energy
$$
\begin{array}{l}
\text { or } \frac{1}{2} M v^{2}=\mu R \cdot d \\
\text { or } \frac{1}{2} \times 0.25 \times 400=\mu \times 0.25 \times 9.8 \times 40 \\
\Rightarrow \mu=\frac{200}{9.8 \times 40}=0.51
\end{array}
$$

By conservation of momentum
$$
\begin{array}{l}
m_{1} u_{1}+m_{2} u_{2}=m_{1} v_{1}+m_{2} v_{2} \\
\Rightarrow 0.02 \times 250+0.23 \times 0=0.02 v+0.23 v \\
5+0=v(0.25) \text { or } v=20 \mathrm{~ms}^{-1}
\end{array}
$$
Now, by conservation of energy
$$
\begin{array}{l}
\text { or } \frac{1}{2} M v^{2}=\mu R \cdot d \\
\text { or } \frac{1}{2} \times 0.25 \times 400=\mu \times 0.25 \times 9.8 \times 40 \\
\Rightarrow \mu=\frac{200}{9.8 \times 40}=0.51
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.