Search any question & find its solution
Question:
Answered & Verified by Expert
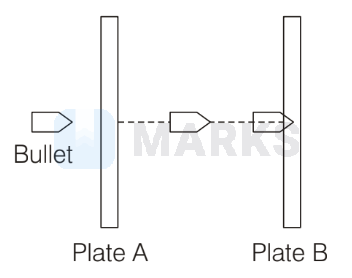
A bullet of mass $10 \mathrm{~g}$ pierces through a plate $A$ of mass $500 \mathrm{~g}$ and then gets embedded into a second plate $B$ of mass $1.49 \mathrm{~kg}$ as shown in the figure. Initially, the two plates $A$ and $B$ are at rest and move with same velocity after collision. The percentage loss in the initial kinetic energy of the bullet, when it is between the plates $A$ and $B$ is _______
(Neglect any loss of material of the plates during the collision)
[QUESTION]
Options:
(Neglect any loss of material of the plates during the collision)
[QUESTION]

Solution:
2807 Upvotes
Verified Answer
The correct answer is:
43.75
Let $v_1$ be the initial velocity of bullet and $v_2$ be the velocity with which each plate moves.
So, applying law of conservation of momentum,
$$
\begin{aligned}
& m v_1=M_1 v_2+\left(M_2+m\right) v_2 \\
& 0.01 v_1=0.5 v_2+(1.49+0.01) v_2
\end{aligned}
$$
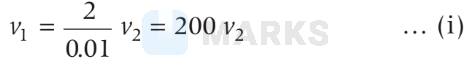
Let $v_3$ be the velocity of bullet, when it comes out of plate $M$.
So, momentum of bullet between plate $M_1$ and $M_2$ = Sum of momentum of plate $M_2$ and bullet.
$$
\begin{aligned}
m v_3 & =\left(M_2+m\right) v_2 \\
0.01 v_3 & =(1.49+0.01) v_2=1.5 v_2
\end{aligned}
$$
$\begin{aligned} \% \text { loss in } \mathrm{KE} & =\frac{(1 / 2) m v_1^2-(1 / 2) m v_3^3}{(1 / 2) m v_1^2} \times 100 \\ & =\frac{v_1^2-v_3^2}{v_1^2} \times 100\end{aligned}$
$\begin{aligned} & =\left\{1-\left(\frac{v_3}{v_1}\right)^2\right\} \times 100 \\ & =\left\{1-\left(\frac{150}{200}\right)^2\right\} \times 100 \\ & =\left(1-\frac{9}{16}\right) \times 100=\frac{7}{16} \times 100=\frac{7}{4} \times 25 \\ & =43.75 \%\end{aligned}$
So, applying law of conservation of momentum,
$$
\begin{aligned}
& m v_1=M_1 v_2+\left(M_2+m\right) v_2 \\
& 0.01 v_1=0.5 v_2+(1.49+0.01) v_2
\end{aligned}
$$
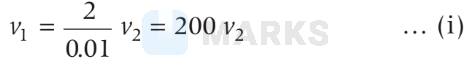
Let $v_3$ be the velocity of bullet, when it comes out of plate $M$.
So, momentum of bullet between plate $M_1$ and $M_2$ = Sum of momentum of plate $M_2$ and bullet.
$$
\begin{aligned}
m v_3 & =\left(M_2+m\right) v_2 \\
0.01 v_3 & =(1.49+0.01) v_2=1.5 v_2
\end{aligned}
$$

$\begin{aligned} \% \text { loss in } \mathrm{KE} & =\frac{(1 / 2) m v_1^2-(1 / 2) m v_3^3}{(1 / 2) m v_1^2} \times 100 \\ & =\frac{v_1^2-v_3^2}{v_1^2} \times 100\end{aligned}$
$\begin{aligned} & =\left\{1-\left(\frac{v_3}{v_1}\right)^2\right\} \times 100 \\ & =\left\{1-\left(\frac{150}{200}\right)^2\right\} \times 100 \\ & =\left(1-\frac{9}{16}\right) \times 100=\frac{7}{16} \times 100=\frac{7}{4} \times 25 \\ & =43.75 \%\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.