Let us consider the figure below,


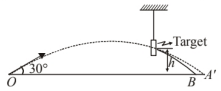
(b) Let $(\text { K.E. })_f(\text { K.E. })_i$ are the kinetic energy of bullet before and after hitting the target.
Conserving energy between ' $O$ ' and ' $A$ '.
$$
\begin{aligned}
&U_i+K_i=U_f+K_f \\
&0+\frac{1}{2} m v^2=m g h+\frac{1}{2} m v^{\prime} \\
&\left(\frac{\left(v^{\prime}\right)^2}{2}\right)=\left(\frac{v^2}{2}-g h\right) \\
&\left(v^{\prime}\right)^2=v^2-2 g h \Rightarrow v^{\prime}=\sqrt{v^2-2 g h}
\end{aligned}
$$
where $v^{\prime}$ is speed of the bullet just before hitting the target. Let us consider speed after emerging from the target is $v$ "then, as given that,
$$
\begin{aligned}
&\frac{1}{2}\left(m v^{\prime \prime}\right)^2=\frac{1}{2}\left[\frac{1}{2} m\left(v^{\prime}\right)^2\right] \\
&\Rightarrow \frac{1}{2} m\left(v^{\prime \prime}\right)^2=\frac{1}{4} m\left(v^{\prime}\right)^2=\frac{1}{4} m\left[v^2-2 g h\right] \\
&\Rightarrow\left(v^{\prime \prime}\right)^2=\frac{v^2-2 g h}{2} \\
&v^{\prime \prime}=\sqrt{\frac{v^2-2 g h}{2}}=\left(\frac{\sqrt{v^2-2 g h}}{\sqrt{2}}\right)
\end{aligned}
$$
From Eqs. (i) and (ii),
$$
\begin{aligned}
&\frac{v^{\prime}}{v^{\prime \prime}}=\frac{\sqrt{v^2-2 g h}}{\frac{\sqrt{v^2-2 g h}}{\sqrt{2}}}=\sqrt{2} \\
&v^{\prime \prime}=\frac{v^{\prime}}{\sqrt{2}} \\
&v^{\prime \prime}=\frac{\sqrt{2} v^{\prime}}{\sqrt{2 \times \sqrt{2}}}=\left(\frac{v^{\prime} \sqrt{2}}{2}\right)
\end{aligned}
$$
So, $v^{\prime \prime}=0.707 v^{\prime}$
Hence, velocity of the bullet $\left(v^{\prime \prime}\right)$ after target is more than half of its earlier velocity $v^{\prime}$.
(d) As the path of bullet after target, will be new parabola because the velocity of the bullet changes to $v^{\prime}$ which is less than $v$, hence, path, followed will change and the bullet reaches at point $B$ instead of $A^{\prime}$.