Search any question & find its solution
Question:
Answered & Verified by Expert
A circle cuts a chord of length 4 a on the $x$ -axis and passes through a point on the $y$ -axis, distant $2 \mathrm{~b}$ from the origin. Then the locus of the centre of this circle, is:
Options:
Solution:
1335 Upvotes
Verified Answer
The correct answer is:
a parabola
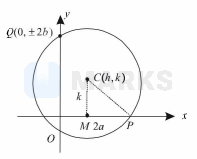
Let centre be $C(h, k)$
$C Q=C P=r$
$\Rightarrow C Q^{2}=C P^{2}$
$(h-0)^{2}+(k \pm 0)^{2}=C M^{2}+M P^{2}$
$h^{2}+(k \pm 2 \mathrm{~b})^{2}=k^{2}+4 a^{2}$
$h^{2}+k^{2}+4 b^{2} \pm 4 b k=k^{2}+4 a^{2}$
Then, the locus of centre $C(h, k)$
$x^{2}+4 b^{2} \pm 4 b y=4 a^{2}$
Hence, the above locus of the centre of circle is a
parabola.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.