Search any question & find its solution
Question:
Answered & Verified by Expert
A circle is inscribed in an equilateral triangle of side of length 12 . If the area and perimeter of any square inscribed in this circle are $m$ and $n$, respectively, then $m+n^2$ is equal to
Options:
Solution:
2437 Upvotes
Verified Answer
The correct answer is:
408
$\because \mathrm{r}=\frac{\Delta}{\mathrm{s}}=\frac{\sqrt{3} \mathrm{a}^2}{4 \cdot \frac{3 \mathrm{a}}{2}}=\frac{\mathrm{a}}{2 \sqrt{3}}=\frac{12}{2 \sqrt{3}}=2 \sqrt{3}$
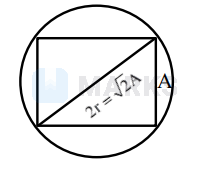
$\begin{aligned} & \therefore A=\mathrm{r} \sqrt{2}=2 \sqrt{6} \\ & \text { Area }=\mathrm{m}=\mathrm{A}^2=24 \\ & \text { Perimeter }=\mathrm{n}=4 \mathrm{~A}=8 \sqrt{6} \\ & \therefore \mathrm{m}+\mathrm{n}^2=24+384 \\ & =408\end{aligned}$

$\begin{aligned} & \therefore A=\mathrm{r} \sqrt{2}=2 \sqrt{6} \\ & \text { Area }=\mathrm{m}=\mathrm{A}^2=24 \\ & \text { Perimeter }=\mathrm{n}=4 \mathrm{~A}=8 \sqrt{6} \\ & \therefore \mathrm{m}+\mathrm{n}^2=24+384 \\ & =408\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.