Search any question & find its solution
Question:
Answered & Verified by Expert
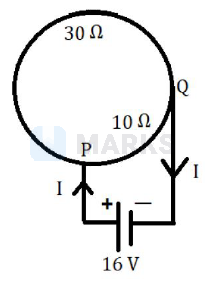
A circular coil of radius 'R' has a resistance of $40 \Omega$. Figure shows two points 'P' and 'Q' on the circumference separated by a distance $\frac{\pi \mathrm{R}}{2}$, which are connected to a $16 \mathrm{~V}$ battery with internal resistance of $0.5 \Omega$. What is the value of current 'I' flowing through the circuit?
Options:

Solution:
1892 Upvotes
Verified Answer
The correct answer is:
2A
The total resistance between points $\mathrm{P}$ and $\mathrm{Q}$.
$\begin{array}{l}
\mathrm{RPQ}=(30 \| 10+0.5) \\
=\frac{30 \times 10}{30+10}+0.5=8 \Omega
\end{array}$
The current flowing through the circuit,
$\begin{array}{l}
V=I R_{P Q} \\
\Rightarrow I=\frac{V}{R_{P Q}}
\end{array}$
where, $V$ is the voltage of source.
$\therefore \mathrm{I}=\frac{16 \mathrm{~V}}{8 \Omega}=2 \mathrm{~A}$
$\begin{array}{l}
\mathrm{RPQ}=(30 \| 10+0.5) \\
=\frac{30 \times 10}{30+10}+0.5=8 \Omega
\end{array}$
The current flowing through the circuit,
$\begin{array}{l}
V=I R_{P Q} \\
\Rightarrow I=\frac{V}{R_{P Q}}
\end{array}$
where, $V$ is the voltage of source.
$\therefore \mathrm{I}=\frac{16 \mathrm{~V}}{8 \Omega}=2 \mathrm{~A}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.