Search any question & find its solution
Question:
Answered & Verified by Expert
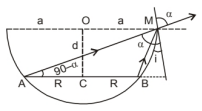
A circular disc of radius $\mathrm{R}$ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius a figure. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index $\mu$ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?

Solution:
2128 Upvotes
Verified Answer
According to the given figure, $\mathrm{AM}$ is the direction of incidence ray before liquid is filled. After liquid is filled in, BM is the direction of the incident ray. Refracted ray in both cases is same as that along AM. MN is tangent at M, so $\mathrm{MN} \perp \mathrm{AB}$ i.e., $\angle \mathrm{N}=90^{\circ}$
Consider the disc is separated by $\mathrm{O}$ at a distance $\mathrm{d}$ as shown in figure given below,
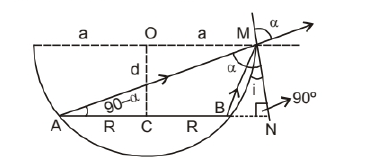
Now let us consider an angle at
$$
\begin{aligned}
(\mathrm{N}) &=90^{\circ}, \\
\mathrm{OM} &=\mathrm{a} \\
\mathrm{NB} &=\mathrm{a}-\mathrm{R}, \\
\mathrm{MB} &=\sqrt{\mathrm{d}^2+(\mathrm{a}-\mathrm{R})^2}
\end{aligned}
$$
From, above figure,
$$
\begin{aligned}
&\sin \mathrm{i}=\left[\frac{\mathrm{NB}}{\mathrm{MB}}\right]=\frac{a-R}{\sqrt{\mathrm{d}^2+(a-R)^2}} \\
&\because \quad \mathrm{AN}=\mathrm{AB}+\mathrm{BN}=2 \mathrm{R}+\mathrm{a}-\mathrm{R}=(\mathrm{a}+\mathrm{R}) \\
&A M=\sqrt{d^2+(a+R)^2} \\
&\text { And, } \quad \sin \mathrm{r}=\cos (90-\alpha) \\
&=\left[\frac{A N}{A M}\right]=\frac{a+R}{\sqrt{d^2+(a+R)^2}} \\
&
\end{aligned}
$$
So, $\quad{ }_1 \mu_0=\frac{\mu_0}{\mu_1}=\frac{\sin \mathrm{i}}{\sin \mathrm{r}}$
$\left(\mu_0\right.$ for air = 1) \& ( $\mu_1$ for liquid)
So, $\quad \frac{1}{\mu}=\frac{\sin i}{\sin r}$
By putting the values of $\sin$ i $\& \sin \mathrm{r}$ we get the distance
(d) is
$$
d=\frac{\mu\left(a^2-b^2\right)}{\sqrt{(a+r)^2-\mu(a-r)^2}}
$$
This is the required expression.
Consider the disc is separated by $\mathrm{O}$ at a distance $\mathrm{d}$ as shown in figure given below,

Now let us consider an angle at
$$
\begin{aligned}
(\mathrm{N}) &=90^{\circ}, \\
\mathrm{OM} &=\mathrm{a} \\
\mathrm{NB} &=\mathrm{a}-\mathrm{R}, \\
\mathrm{MB} &=\sqrt{\mathrm{d}^2+(\mathrm{a}-\mathrm{R})^2}
\end{aligned}
$$
From, above figure,
$$
\begin{aligned}
&\sin \mathrm{i}=\left[\frac{\mathrm{NB}}{\mathrm{MB}}\right]=\frac{a-R}{\sqrt{\mathrm{d}^2+(a-R)^2}} \\
&\because \quad \mathrm{AN}=\mathrm{AB}+\mathrm{BN}=2 \mathrm{R}+\mathrm{a}-\mathrm{R}=(\mathrm{a}+\mathrm{R}) \\
&A M=\sqrt{d^2+(a+R)^2} \\
&\text { And, } \quad \sin \mathrm{r}=\cos (90-\alpha) \\
&=\left[\frac{A N}{A M}\right]=\frac{a+R}{\sqrt{d^2+(a+R)^2}} \\
&
\end{aligned}
$$
So, $\quad{ }_1 \mu_0=\frac{\mu_0}{\mu_1}=\frac{\sin \mathrm{i}}{\sin \mathrm{r}}$
$\left(\mu_0\right.$ for air = 1) \& ( $\mu_1$ for liquid)
So, $\quad \frac{1}{\mu}=\frac{\sin i}{\sin r}$
By putting the values of $\sin$ i $\& \sin \mathrm{r}$ we get the distance
(d) is
$$
d=\frac{\mu\left(a^2-b^2\right)}{\sqrt{(a+r)^2-\mu(a-r)^2}}
$$
This is the required expression.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.