Search any question & find its solution
Question:
Answered & Verified by Expert
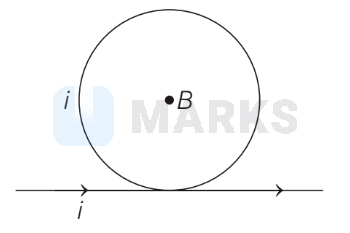
A circular loop and an infinitely long straight conductor carry equal currents, as shown in the figure. The net magnetic field at the centre of the loop is $B_1$, when the current in the loop is clockwise and $B_2$ when the current in the loop is anti-clockwise. Then $\frac{B_1}{B_2}$ is
Options:

Solution:
2768 Upvotes
Verified Answer
The correct answer is:
$\frac{15}{29}$
When current is clockwise, then net magnetic field,
$$
B_1=\frac{\mu_0 i}{2 r}-\frac{\mu_0 i}{2 \pi r} \Rightarrow B_1=\frac{\mu_0 i}{2 r}\left(1-\frac{1}{\pi}\right)
$$
Similarly, when current is anti-clockwise
$$
B_2=\frac{\mu_0 i}{2 r}\left(1+\frac{1}{\pi}\right)
$$
Now, $\frac{B_1}{B_2}=\frac{\frac{\pi-1}{\pi}}{\frac{\pi+1}{\pi}}=\frac{\frac{22}{7}-1}{\frac{22}{7}+1} \Rightarrow \frac{B_1}{B_2}=\frac{15}{29}$
$$
B_1=\frac{\mu_0 i}{2 r}-\frac{\mu_0 i}{2 \pi r} \Rightarrow B_1=\frac{\mu_0 i}{2 r}\left(1-\frac{1}{\pi}\right)
$$
Similarly, when current is anti-clockwise
$$
B_2=\frac{\mu_0 i}{2 r}\left(1+\frac{1}{\pi}\right)
$$
Now, $\frac{B_1}{B_2}=\frac{\frac{\pi-1}{\pi}}{\frac{\pi+1}{\pi}}=\frac{\frac{22}{7}-1}{\frac{22}{7}+1} \Rightarrow \frac{B_1}{B_2}=\frac{15}{29}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.