Search any question & find its solution
Question:
Answered & Verified by Expert
A circular metal plate of radius $R$ is rotating with a uniform angular velocity $\omega$ with its plane perpendicular to a uniform magnetic field $B$. Then the emf developed between the centre and the rim of the plate is
Options:
Solution:
2717 Upvotes
Verified Answer
The correct answer is:
$\omega B R^2 / 2$
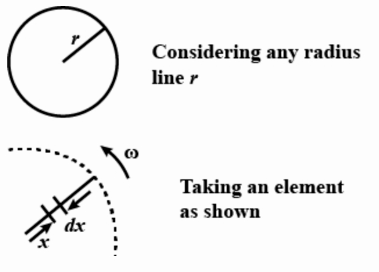
We write $d \in=\operatorname{Blv}(\epsilon \mathrm{HF})$
Now l $=\mathrm{dx} \mathrm{v}=\omega \mathrm{x}$
$\int \mathrm{d} \in=\mathrm{B} \omega \int_0^r \mathrm{x} d x$
$\in=\frac{\mathrm{B} \omega \mathrm{r}^2}{2}$
Now l $=\mathrm{dx} \mathrm{v}=\omega \mathrm{x}$
$\int \mathrm{d} \in=\mathrm{B} \omega \int_0^r \mathrm{x} d x$
$\in=\frac{\mathrm{B} \omega \mathrm{r}^2}{2}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.