Consider a small circular element of thickness $d r$ at a distance $r$ from the centre of spiral as shown in the figure,


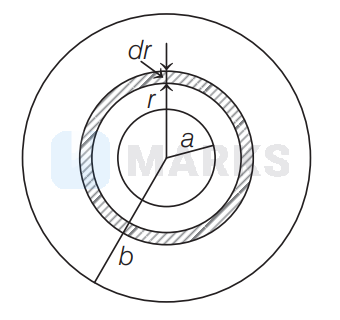
Total number of turns in this element $=\frac{N}{b-a} d r$ Current passing through this element,
$i=\frac{N}{b-a} d r I$
$\therefore$ Magnetic field at the centre of spiral due to this element is given as
$d B=\frac{\mu_0 i}{2 r}=\frac{\mu_0}{2 r} \cdot \frac{N I}{b-a} d r$
$\therefore$ Total magnetic field,
$B=\int d B=nt_a^b \frac{\mu_0 N I}{2(b-a)} \cdot \frac{d r}{r}$
$\Rightarrow \quad B=\frac{\mu_0 N I}{2(b-a)} \ln \left(\frac{b}{a}\right)$
Given, $N=100, I=1 \mathrm{~A}, a=1 \mathrm{~cm}=10^{-2} \mathrm{~m}$, $b=2 \mathrm{~cm}=2 \times 10^{-2} \mathrm{~m}$
$\therefore \quad B=\frac{4 \pi \times 10^{-7} \times 100 \times 1}{2\left(2 \times 10^{-2}-1 \times 10^{-2}\right)} \ln \left(\frac{2 \times 10^{-2}}{1 \times 10^{-2}}\right)$
$=2 \pi \times 10^{-3} \ln (2)$
$=2 \pi \ln (2) \times 10^{-3} \mathrm{~T}$
$=2 \pi \ln (2) \mathrm{mT}$