Search any question & find its solution
Question:
Answered & Verified by Expert
A coil in the shape of an equilateral triangle of side $l$ is suspended between the pole pieces of a permanent magnet such that $\overrightarrow{\mathbf{B}}$ is in plane of the coil. If due to a current $i$ in the triangle a torque $\tau$ acts on it, the side $l$ of the triangle is
Options:
Solution:
1840 Upvotes
Verified Answer
The correct answer is:
$2\left(\frac{\tau}{\sqrt{3} B i}\right)^{1 / 2}$
Torque acting on equilateral triangle in a magnetic field $\overrightarrow{\mathbf{B}}$ is
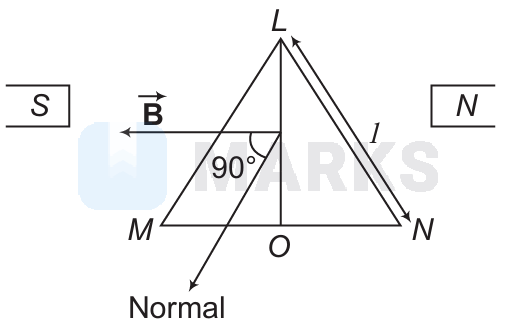
$\tau=i A B \sin \theta$
Area of triangle LMN $A=\frac{\sqrt{3}}{4} l^2$ and $\theta=90^{\circ}$
Substituting the given values in the expression for torque, we have
$\begin{aligned}\tau & =i \times \frac{\sqrt{3}}{4} l^2 B \sin 90^{\circ} \\& =\frac{\sqrt{3}}{4} i l^2 B\left(\because \sin 90^{\circ}=1\right)\end{aligned}$
Hence, $l=2\left(\frac{\tau}{\sqrt{3} B i}\right)^{1 / 2}$

$\tau=i A B \sin \theta$
Area of triangle LMN $A=\frac{\sqrt{3}}{4} l^2$ and $\theta=90^{\circ}$
Substituting the given values in the expression for torque, we have
$\begin{aligned}\tau & =i \times \frac{\sqrt{3}}{4} l^2 B \sin 90^{\circ} \\& =\frac{\sqrt{3}}{4} i l^2 B\left(\because \sin 90^{\circ}=1\right)\end{aligned}$
Hence, $l=2\left(\frac{\tau}{\sqrt{3} B i}\right)^{1 / 2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.