Search any question & find its solution
Question:
Answered & Verified by Expert
A compound slab is made of two parallel plates of copper and brass of the same thickness and having thermal conductivities in the ratio $4: 1$. The free face of copper is at $0^{\circ} \mathrm{C}$. The temperature of the interface is $20^{\circ} \mathrm{C}$. What is the temperature of the free face of brass?
Options:
Solution:
2610 Upvotes
Verified Answer
The correct answer is:
$100^{\circ} \mathrm{C}$
Given, $K_{\text {copper }}: K_{\text {brass }}=4: 1$
$$
\Rightarrow \quad \frac{K_{\text {copper }}}{K_{\text {brass }}}=\frac{4}{1}
$$
Let the temperature of the free surface of brass $=\theta$
Rate of flow of heat will be equal in both the plates as connected in series.
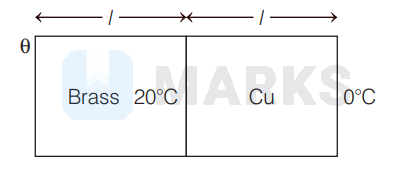
i.e. $H=K_{\text {brass }} \frac{A(\theta-20)}{l}=K_{\text {copper }} \frac{A(20-0)}{l}$
$$
\begin{array}{cl}
\Rightarrow \quad \frac{\theta-20}{20} & =\frac{K_{\text {copper }}}{K_{\text {brass }}}=\frac{4}{1} \\
\Rightarrow \quad \theta-20 & =80 \\
\theta & =100^{\circ} \mathrm{C}
\end{array}
$$
$$
\Rightarrow \quad \frac{K_{\text {copper }}}{K_{\text {brass }}}=\frac{4}{1}
$$
Let the temperature of the free surface of brass $=\theta$
Rate of flow of heat will be equal in both the plates as connected in series.

i.e. $H=K_{\text {brass }} \frac{A(\theta-20)}{l}=K_{\text {copper }} \frac{A(20-0)}{l}$
$$
\begin{array}{cl}
\Rightarrow \quad \frac{\theta-20}{20} & =\frac{K_{\text {copper }}}{K_{\text {brass }}}=\frac{4}{1} \\
\Rightarrow \quad \theta-20 & =80 \\
\theta & =100^{\circ} \mathrm{C}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.