Search any question & find its solution
Question:
Answered & Verified by Expert
A conducting sphere $S_1$ of radius $r_1$ is connected by a conducting wire to another conducting sphere $S_2$ of radius $r_2$, where $r_1=3 \mathrm{~cm}$ and $r_2=2$ $\mathrm{cm}$. Before they are connected, $s_1$ carries charge of 10 units. The electric potential at the point which is at a distance $4 \mathrm{~cm}$ from the centre of $S_1$ and a distance $3 \mathrm{~cm}$ from the centre of $S_2$ is
Options:
Solution:
2834 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{4 \pi \varepsilon_0} \frac{17}{6}$
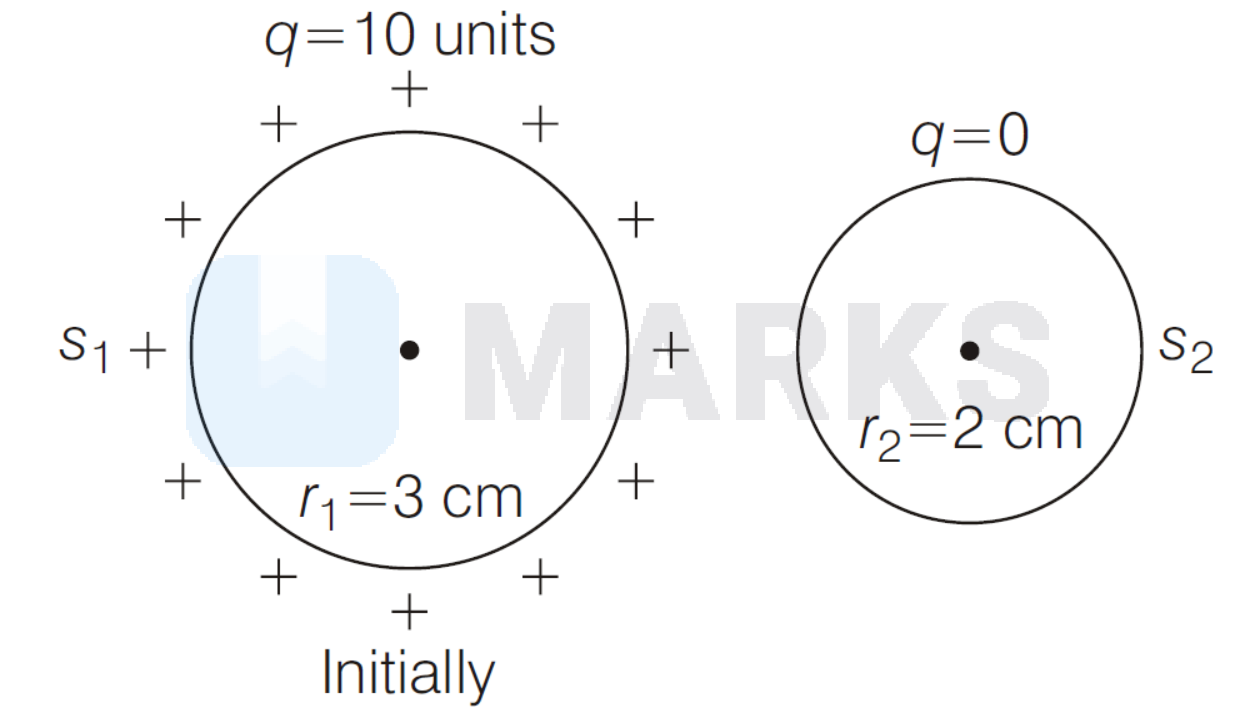
When spheres are connected, charges are redistributed such that potential on their surfaces are same.
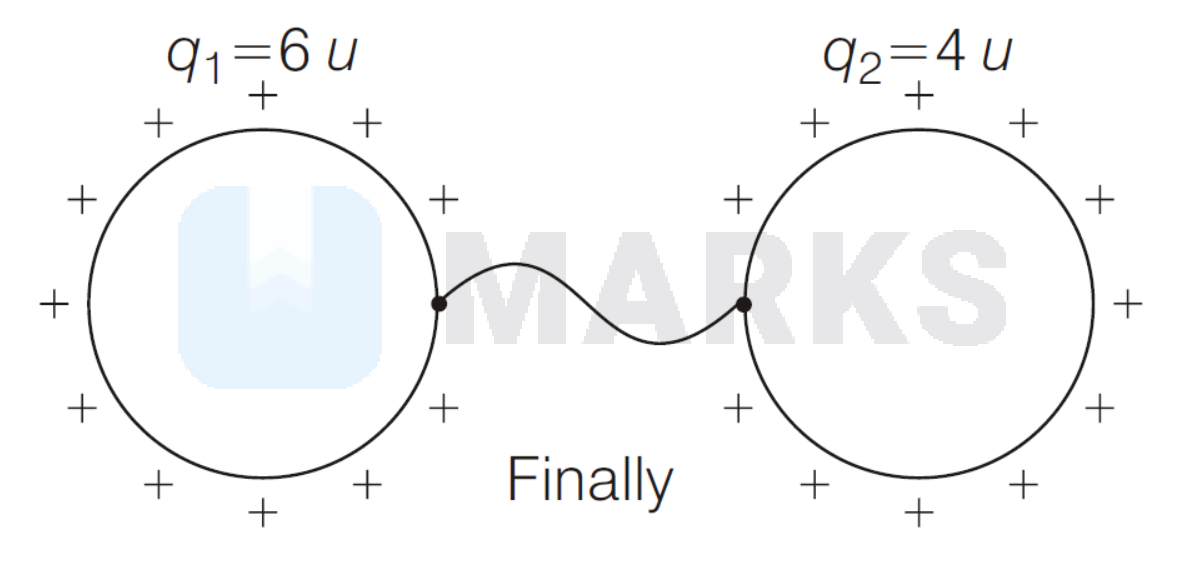
So, we have
$$
\begin{aligned}
q_1+q_2 & =10 \\
\frac{k q_1}{r_1} & =\frac{k q_2}{r_2} \Rightarrow \frac{q_1}{3}=\frac{q_2}{2}
\end{aligned}
$$
and
$$
\frac{k q_1}{r_1}=\frac{k q_2}{r_2} \Rightarrow \frac{q_1}{3}=\frac{q_2}{2}
$$
Hence, $q_1=6$ units and $q_2=4$ units.
Now, potential at some point $P$ distant $4 \mathrm{~cm}$ from $s_1$ and $3 \mathrm{~cm}$ from $s_2$ is
$$
\begin{aligned}
V & =\frac{k q_1}{r_1}+\frac{k q_2}{r_2}=k \frac{6}{4}+k \frac{4}{3} \\
& =k\left(\frac{3}{2}+\frac{4}{3}\right)=k \frac{17}{6} V=\frac{1}{4 \pi \varepsilon_0} \frac{17}{6} V
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.