Search any question & find its solution
Question:
Answered & Verified by Expert
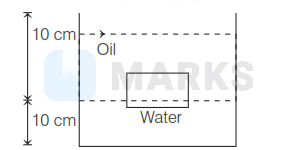
A cubical block of wood, of length $10 \mathrm{~cm}$, floats at the interface between oil of density $800 \mathrm{~kg} / \mathrm{m}^3$ and water. The lower surface of the block is $1.5 \mathrm{~cm}$ below the interface. If the depth of water is $10 \mathrm{~cm}$ below the interface and oil is upto $10 \mathrm{~cm}$ above the interface then the difference in pressure at the lower and the upper face of the wooden block is
(Assume density of water, $\rho=1000 \mathrm{~kg} / \mathrm{m}^3$ and acceleration of gravity, $g=10 \mathrm{~m} / \mathrm{s}^2$ )
Options:
(Assume density of water, $\rho=1000 \mathrm{~kg} / \mathrm{m}^3$ and acceleration of gravity, $g=10 \mathrm{~m} / \mathrm{s}^2$ )

Solution:
2738 Upvotes
Verified Answer
The correct answer is:
$830 \mathrm{~Pa}$
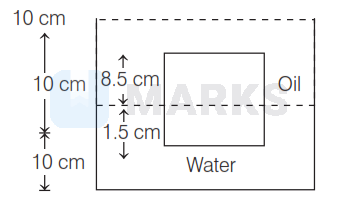
Given, length of cubical block, $l=10 \mathrm{~cm}=0.1 \mathrm{~m}$
density of oil, $\rho_0=800 \mathrm{~kg} / \mathrm{m}^3$
and density of water, $\rho_w=10^3 \mathrm{~kg} / \mathrm{m}^3$
If $V_1$ and $V_2$ be the volume of wooden block in water and oil respectively, then
$$
\begin{aligned}
V_1: V_2 & =1.5: 8.5 \\
\frac{V_1}{V_2} & =\frac{1.5}{8.5}=\frac{3}{17} \\
\therefore \quad V_1 & =\frac{3}{17} V_2
\end{aligned}
$$
$\therefore V_1+V_2=V$, where, $V$ is the volume of the block.
From Eq. (i), we get
$$
\begin{array}{rlrl}
& \frac{3}{17} V_2+V_2 & =V \Rightarrow V_2=\frac{17}{20} \mathrm{~V} \\
\therefore \quad V_1 & =\frac{3}{20} \mathrm{~V}
\end{array}
$$
If $\rho$ be the density of the block.
$\therefore$ weight of block $=$ weight of oil displaced + weight of water displaced
$$
\begin{gathered}
V \rho G=V_1 \rho_\omega g+V_2 \rho_{\text {oil }} g \\
V \rho g=\frac{3}{20} V \rho_w g+\frac{17}{20} V \rho_{\text {oil }} g \\
\rho=\frac{3}{20} \rho_w+\frac{17}{20} \rho_{\text {oil }}=\frac{3}{20} \times 1000+\frac{17}{20} \times 800 \\
=830 \mathrm{~kg} / \mathrm{m}^3
\end{gathered}
$$
$\therefore$ Pressure difference
$$
p=\rho g h=830 \times 10 \times 0.1=830 \mathrm{~Pa}
$$

density of oil, $\rho_0=800 \mathrm{~kg} / \mathrm{m}^3$
and density of water, $\rho_w=10^3 \mathrm{~kg} / \mathrm{m}^3$
If $V_1$ and $V_2$ be the volume of wooden block in water and oil respectively, then
$$
\begin{aligned}
V_1: V_2 & =1.5: 8.5 \\
\frac{V_1}{V_2} & =\frac{1.5}{8.5}=\frac{3}{17} \\
\therefore \quad V_1 & =\frac{3}{17} V_2
\end{aligned}
$$
$\therefore V_1+V_2=V$, where, $V$ is the volume of the block.
From Eq. (i), we get
$$
\begin{array}{rlrl}
& \frac{3}{17} V_2+V_2 & =V \Rightarrow V_2=\frac{17}{20} \mathrm{~V} \\
\therefore \quad V_1 & =\frac{3}{20} \mathrm{~V}
\end{array}
$$
If $\rho$ be the density of the block.
$\therefore$ weight of block $=$ weight of oil displaced + weight of water displaced
$$
\begin{gathered}
V \rho G=V_1 \rho_\omega g+V_2 \rho_{\text {oil }} g \\
V \rho g=\frac{3}{20} V \rho_w g+\frac{17}{20} V \rho_{\text {oil }} g \\
\rho=\frac{3}{20} \rho_w+\frac{17}{20} \rho_{\text {oil }}=\frac{3}{20} \times 1000+\frac{17}{20} \times 800 \\
=830 \mathrm{~kg} / \mathrm{m}^3
\end{gathered}
$$
$\therefore$ Pressure difference
$$
p=\rho g h=830 \times 10 \times 0.1=830 \mathrm{~Pa}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.