Search any question & find its solution
Question:
Answered & Verified by Expert
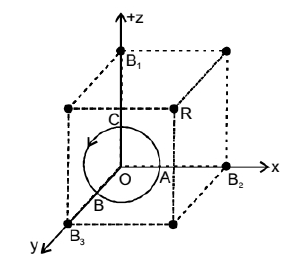
A current carrying loop consists of 3 identical quarter circles of radius $R$, lying in the positive quadrants of the $x$ $-y, y-z$ and $z-x$ planes with their centres at the origin, joined together. Find the direction and magnitude of $\mathrm{B}$ at the origin.
Solution:
1923 Upvotes
Verified Answer
The magnetic field due to arc of current carrying coil which subtends an angle $\theta$ at centre is given by
$$
\mathrm{B}=\frac{\mu_0}{4 \pi} \frac{I \theta}{\mathrm{R}}
$$
The magnetic field for the current carrying loop quarter circles of radius $R$, lying in the positive quadrants of the $x$ y plane
when $\left(\theta=\frac{\pi}{2}\right)$
$$
\mathrm{B}_1=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}\left(\frac{\pi}{2}\right)}{\mathrm{R}} \hat{\mathrm{k}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}}{2 \mathrm{R}} \hat{\mathrm{k}}=\frac{\mu_0 \mathrm{I}}{8 \pi \mathrm{R}} \hat{\mathrm{k}}
$$
The magnetic field for the current carrying loop quarter circles of radius $R$. lying in the positive quadrants of the $y-z$ plane
$$
B_2=\frac{\mu_0}{4 \pi} \frac{I}{2 R} \hat{\mathrm{i}}=\frac{\mu_0 \mathrm{I}}{8 \pi \mathrm{R}} \hat{\mathrm{i}}
$$
The magnetic field for the current carrying loop quarter circles of radius R, lying in the positive quadrants of the zxplane.
$$
\mathrm{B}_3=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}}{2 \mathrm{R}} \hat{\mathrm{j}}=\frac{\mu_0 \mathrm{I}}{8 \pi \mathrm{R}} \hat{\mathrm{j}}
$$
Current carrying loop consists of 3 identical quarter circles of radius $R$, lying in the positive quadrants of the $x-y, y-y$ and $z-z$ planes with their centres at the origin, joined together is equal to the vector sum of magnetic field due to each quarter is
$$
B=\frac{1}{4 \pi}(\hat{i}+\hat{j}+\hat{k}) \frac{\mu_0 I}{2 R}=\frac{\mu_0 I}{8 \pi R}(\hat{i}+\hat{j}+\hat{k})
$$
$$
\mathrm{B}=\frac{\mu_0}{4 \pi} \frac{I \theta}{\mathrm{R}}
$$
The magnetic field for the current carrying loop quarter circles of radius $R$, lying in the positive quadrants of the $x$ y plane
when $\left(\theta=\frac{\pi}{2}\right)$
$$
\mathrm{B}_1=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}\left(\frac{\pi}{2}\right)}{\mathrm{R}} \hat{\mathrm{k}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}}{2 \mathrm{R}} \hat{\mathrm{k}}=\frac{\mu_0 \mathrm{I}}{8 \pi \mathrm{R}} \hat{\mathrm{k}}
$$
The magnetic field for the current carrying loop quarter circles of radius $R$. lying in the positive quadrants of the $y-z$ plane
$$
B_2=\frac{\mu_0}{4 \pi} \frac{I}{2 R} \hat{\mathrm{i}}=\frac{\mu_0 \mathrm{I}}{8 \pi \mathrm{R}} \hat{\mathrm{i}}
$$
The magnetic field for the current carrying loop quarter circles of radius R, lying in the positive quadrants of the zxplane.
$$
\mathrm{B}_3=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}}{2 \mathrm{R}} \hat{\mathrm{j}}=\frac{\mu_0 \mathrm{I}}{8 \pi \mathrm{R}} \hat{\mathrm{j}}
$$
Current carrying loop consists of 3 identical quarter circles of radius $R$, lying in the positive quadrants of the $x-y, y-y$ and $z-z$ planes with their centres at the origin, joined together is equal to the vector sum of magnetic field due to each quarter is

$$
B=\frac{1}{4 \pi}(\hat{i}+\hat{j}+\hat{k}) \frac{\mu_0 I}{2 R}=\frac{\mu_0 I}{8 \pi R}(\hat{i}+\hat{j}+\hat{k})
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.