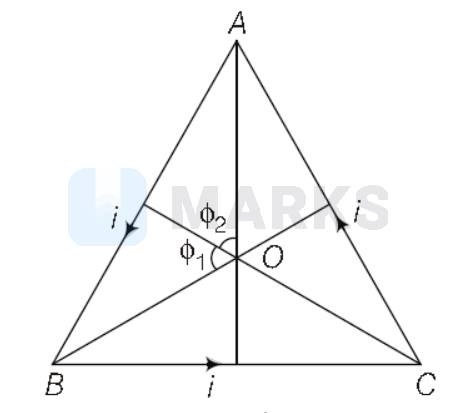
Let the centroid of the triangle is $O$, magnetic field due to side $A B$


$$
B_1=\frac{\mu_0}{4 \pi} \cdot \frac{i}{r}\left(\sin \phi_1+\sin \phi_2\right)
$$
where, $r$ is perpendicular distance of $A B$ from centroid $O$. The magnetic field due to each side is same in magnitude and direction, so the resultant field
$$
\begin{aligned}
& B=3 B_1 \\
&=3 \frac{\mu_0}{4 \pi} \cdot \frac{i}{r}\left(\sin \phi_1+\sin \phi_2\right) \\
& i \quad\left(\text { Here, } \mu_0=4 \pi \times 10^{-7} \mathrm{H} / \mathrm{m}\right) \\
& i
\end{aligned}
$$
In equilateral triangle, $\phi_1=\phi_2=60^{\circ}$
$$
\therefore \quad B=3 \frac{\mu_0}{4 \pi} \cdot \frac{1}{r}\left(\sin 60^{\circ}+\sin 60^{\circ}\right)
$$
Also, $\quad r=4.5 \times 10^{-2} \mathrm{~m}$
$$
\begin{aligned}
\Rightarrow \quad B & =\frac{3 \mu_0}{4 \pi} \cdot \frac{1}{4.5 \times 10^{-2}}\left(\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\right) \mathrm{T} \\
& =\frac{3 \sqrt{3} \cdot \mu_0}{4 \pi} \cdot \frac{1}{4.5 \times 10^{-2}} \mathrm{~T} \\
& =\frac{3 \sqrt{3} \times 10^{-7}}{4.5 \times 10^{-2}} \mathrm{~T} \quad \quad\left[\because \frac{\mu_0}{4 \pi}=10^{-7} \mathrm{~N}^2 \mathrm{~A}^2\right] \\
& =\frac{3 \times 1.73}{4.5} \times 10^{-5} \mathrm{~T} \\
& =1.15 \times 10^{-5} \mathrm{~T} \approx 2 \times 10^{-5} \mathrm{~T}
\end{aligned}
$$