Search any question & find its solution
Question:
Answered & Verified by Expert
A curved surface is shown in figure. The portion $B C D$ is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from $A$ which is at a slightly greater height than $C$.
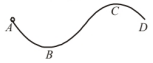
With the surface $A B$, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
(a) For which balls is total mechanical energy conserved?
(b) Which ball (s) can reach $D$ ?
(c) For balls which do not reach $D$, which of the balls can reach back $A$ ?

With the surface $A B$, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
(a) For which balls is total mechanical energy conserved?
(b) Which ball (s) can reach $D$ ?
(c) For balls which do not reach $D$, which of the balls can reach back $A$ ?
Solution:
2743 Upvotes
Verified Answer
(a) As ball 1 is rolling down without slipping, no force of friction acts therefore no loss of energy or there is no dissipation of energy hence, total mechanical energy is conserved.
Ball 3 is having negligible friction hence, there is no loss of energy.
(b) Ball 1 acquires rotational energy, ball 2 has small friction so, loses energy. They cannot cross at $C$. Ball 3 can cross over.
(c) Ball 1,2 turn back before reaching $C$. Because of loss of energy, ball 2 cannot reach back to $A$. Ball 1 has a rotational motion in "wrong" sense when it reaches $B$. So no ball can reach at $A$ due to kinetic friction.
Ball 3 is having negligible friction hence, there is no loss of energy.
(b) Ball 1 acquires rotational energy, ball 2 has small friction so, loses energy. They cannot cross at $C$. Ball 3 can cross over.
(c) Ball 1,2 turn back before reaching $C$. Because of loss of energy, ball 2 cannot reach back to $A$. Ball 1 has a rotational motion in "wrong" sense when it reaches $B$. So no ball can reach at $A$ due to kinetic friction.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.