Search any question & find its solution
Question:
Answered & Verified by Expert
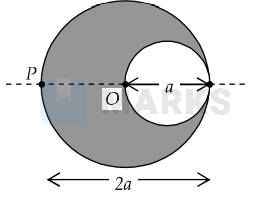
A cylindrical cavity of diameter a exists inside a cylinder of diameter $2 a$ as shown in the figure. Both the cylinder and the cavity are infinity long. A uniform current density $J$ flows along the length. If the magnitude of the magnetic field at the point $P$ is given by $\frac{N}{12} \mu_{0} a J$, then the value of $N$ is

Solution:
2400 Upvotes
Verified Answer
The correct answer is:
5
Current density $J=\frac{\text { current }}{\text { area }}=\frac{I}{A} \Rightarrow I=\mathrm{JA}$ Magnetic field $\mathrm{B}_{\mathrm{R}}$ after removing cavity $(\mathrm{C})$ $\mathrm{B}_{\mathrm{R}}=\mathrm{B}_{\text {total }}-\mathrm{B}_{\text {cavity }}$
$\begin{array}{l}
\frac{\mu_{0} I_{t}}{2 \pi a}-\frac{\mu_{0} I_{c}}{2 \pi\left(\frac{3}{2} a\right)} \\
\quad=\frac{\mu_{0}}{\pi a}\left[\frac{I_{t}}{2}-\frac{I_{c}}{3}\right]\left(\text { here } I_{t}=J\left(\pi a^{2}\right) I_{c}=J\left(\frac{\pi a^{2}}{4}\right)\right) \\
=\frac{\mu_{0}}{\pi a}\left[\frac{\pi a^{2} J}{2}-\frac{\pi a^{2} J}{12}\right] \\
\text { or, } \mathrm{B}_{\mathrm{R}}=\frac{5 \mu_{0} a J}{12}
\end{array}$
Comparing it with $\frac{N}{12} \mu_{0} a J$ We get $N=5$
$\begin{array}{l}
\frac{\mu_{0} I_{t}}{2 \pi a}-\frac{\mu_{0} I_{c}}{2 \pi\left(\frac{3}{2} a\right)} \\
\quad=\frac{\mu_{0}}{\pi a}\left[\frac{I_{t}}{2}-\frac{I_{c}}{3}\right]\left(\text { here } I_{t}=J\left(\pi a^{2}\right) I_{c}=J\left(\frac{\pi a^{2}}{4}\right)\right) \\
=\frac{\mu_{0}}{\pi a}\left[\frac{\pi a^{2} J}{2}-\frac{\pi a^{2} J}{12}\right] \\
\text { or, } \mathrm{B}_{\mathrm{R}}=\frac{5 \mu_{0} a J}{12}
\end{array}$
Comparing it with $\frac{N}{12} \mu_{0} a J$ We get $N=5$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.