Search any question & find its solution
Question:
Answered & Verified by Expert
A cylindrical tank is filled with water to a level of $3 \mathrm{~m}$. A hole is opened at a height of $52.5 \mathrm{~cm}$ from the bottom. The ratio of the area of the hole to that of the cross-sectional area of the tank is 0.1 . The square of the speed with which water will be coming out from the orifice is $\left(g=10 \mathrm{~ms}^{-2}\right)$
Options:
Solution:
2835 Upvotes
Verified Answer
The correct answer is:
$50 \mathrm{~m}^2 \mathrm{~s}^{-2}$
Let $a$ be area of hole, $v_{\varepsilon}$ be the velocity of efflux, $h$ be the height of liquid above the hole. Let $v$ be the speed with which level decreases in the container.
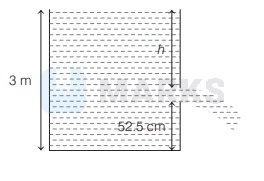
From equation of continuity,
$$
a v_e=A v \Rightarrow v=\frac{a v_e}{A}
$$
Using Bernoulli's theorem,
$$
\begin{array}{rlrl}
& p_0+h \rho g+\frac{1}{2} \rho v^2 & =p_0+\frac{1}{2} \rho v_e^2 \\
\Rightarrow & h \rho g+\frac{1}{2} \rho\left(\frac{a v_e}{A}\right)^2 & =\frac{1}{2} \rho v_e^2 \\
\text { or } & v_e^2=\frac{2 g h}{1-\left(\frac{a^2}{A^2}\right)} & =\frac{2 \times(3-0.525) \times 10}{1-(0.1)^2} \\
\Rightarrow & & v_e^2 & =50 \mathrm{~m}^2 \mathrm{~s}^{-2}
\end{array}
$$

From equation of continuity,
$$
a v_e=A v \Rightarrow v=\frac{a v_e}{A}
$$
Using Bernoulli's theorem,
$$
\begin{array}{rlrl}
& p_0+h \rho g+\frac{1}{2} \rho v^2 & =p_0+\frac{1}{2} \rho v_e^2 \\
\Rightarrow & h \rho g+\frac{1}{2} \rho\left(\frac{a v_e}{A}\right)^2 & =\frac{1}{2} \rho v_e^2 \\
\text { or } & v_e^2=\frac{2 g h}{1-\left(\frac{a^2}{A^2}\right)} & =\frac{2 \times(3-0.525) \times 10}{1-(0.1)^2} \\
\Rightarrow & & v_e^2 & =50 \mathrm{~m}^2 \mathrm{~s}^{-2}
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.