Search any question & find its solution
Question:
Answered & Verified by Expert
A deflection magnetometer is adjusted in the usual way. When a magnet is introduced, the deflection observed is $\theta$, and the period of oscillation of the needle in the magnetometer is $T$. When the magnet is removed, the period of oscillation is $T_0$. The relation between $T$ and $T_0$ is
Options:
Solution:
1529 Upvotes
Verified Answer
The correct answer is:
$T^2=T_0^2 \cos \theta$
In the usual setting of deflection magnetometer, field due to magnet $(F)$ and horizontal component $(H)$ of earth's field are perpendicular to each other. Therefore, the net field on the magnetic needle is $\sqrt{F^2+H^2}$
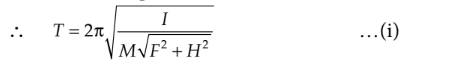
When the magnet is removed,
Also, $\frac{F}{H}=\tan \theta$
Dividing (i) by (ii), we get
$\begin{aligned} & \frac{T}{T_0}=\sqrt{\frac{H}{\sqrt{F^2+H^2}}} \\ = & \sqrt{\frac{H}{\sqrt{H^2 \tan ^2 \theta+H^2}}}=\sqrt{\frac{H}{H \sqrt{\sec ^2 \theta}}}=\sqrt{\cos \theta} \\ \Rightarrow & \frac{T^2}{T_0^2}=\cos \theta \quad \therefore \quad T^2=T_0^2 \cos \theta\end{aligned}$
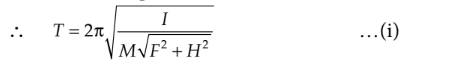
When the magnet is removed,

Also, $\frac{F}{H}=\tan \theta$
Dividing (i) by (ii), we get
$\begin{aligned} & \frac{T}{T_0}=\sqrt{\frac{H}{\sqrt{F^2+H^2}}} \\ = & \sqrt{\frac{H}{\sqrt{H^2 \tan ^2 \theta+H^2}}}=\sqrt{\frac{H}{H \sqrt{\sec ^2 \theta}}}=\sqrt{\cos \theta} \\ \Rightarrow & \frac{T^2}{T_0^2}=\cos \theta \quad \therefore \quad T^2=T_0^2 \cos \theta\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.