Search any question & find its solution
Question:
Answered & Verified by Expert
A dietician wishes to mix together two kinds of food $X$ and $Y$ in such a way that the mixture contains at least 10 units of vitamin $A, 12$ units of vitamin $B$ and 8 units of vitamin C. The vitamin contents of one kg food is given below:
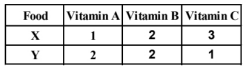
One kg of food $X$ costs ₹ 16 and one kg of food $Y$ costs $₹ 20$. Find the least cost of the mixture which will produce the required diet?

One kg of food $X$ costs ₹ 16 and one kg of food $Y$ costs $₹ 20$. Find the least cost of the mixture which will produce the required diet?
Solution:
1647 Upvotes
Verified Answer
Let there be $x \mathrm{~kg}$ food $\mathrm{X}$ and $\mathrm{y} \mathrm{kg}$ food $\mathrm{Y}$. Objective function $Z=16 x+20 y$, subject to constraints are, $x+2 y \geq 10,2 x+2 y \geq 12$ and $3 x+y \geq, 8, x, y \geq 0$
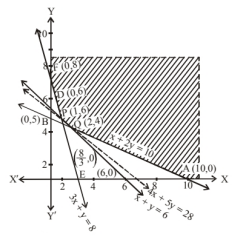
$Z=16 x+20 y$
At $\mathrm{F}(0,8), \quad Z=16 x+20 y=0+160=160$
At $\mathrm{P}(1,5), \quad \mathrm{Z}=16+100=116$
At $\mathrm{Q}(2,4), \quad \mathrm{Z}=32+80=112 \quad \min ^{\mathrm{m}}$
At A $(10,0), \quad \mathrm{Z}=160+0=160$
This shows that minimum value of $\mathrm{z}$ is $₹ 112$ feasible region
is unbounded.
Consider the inequality.
$16 x+20 y < 112$ or $4 x+5 y=28$
The line $4 x+5 y=28$ passes through $(7,0)$ and $\left(0, \frac{28}{5}\right)$.
Also putting $x=0, y=0$ in $4 x+5 y < 28$ we get $0 < 28$ which
$\therefore \quad 8 \mathrm{x}+10 \mathrm{y}=33$ lies below the line $4 \mathrm{x}+5 \mathrm{y}=28$.
Hence there is no common point between feasible region
and $4 x+5 y < 33$
$\Rightarrow$ Minimum value of $\mathrm{Z}=112$ at $\mathrm{x}=2, \mathrm{y}=4$ i.e., least value
of mixture is $₹ 112$ when $2 \mathrm{~kg}$ of food $x$ and $4 \mathrm{~kg}$ of food $y$
are mixed.

$Z=16 x+20 y$
At $\mathrm{F}(0,8), \quad Z=16 x+20 y=0+160=160$
At $\mathrm{P}(1,5), \quad \mathrm{Z}=16+100=116$
At $\mathrm{Q}(2,4), \quad \mathrm{Z}=32+80=112 \quad \min ^{\mathrm{m}}$
At A $(10,0), \quad \mathrm{Z}=160+0=160$
This shows that minimum value of $\mathrm{z}$ is $₹ 112$ feasible region
is unbounded.
Consider the inequality.
$16 x+20 y < 112$ or $4 x+5 y=28$
The line $4 x+5 y=28$ passes through $(7,0)$ and $\left(0, \frac{28}{5}\right)$.
Also putting $x=0, y=0$ in $4 x+5 y < 28$ we get $0 < 28$ which
$\therefore \quad 8 \mathrm{x}+10 \mathrm{y}=33$ lies below the line $4 \mathrm{x}+5 \mathrm{y}=28$.
Hence there is no common point between feasible region
and $4 x+5 y < 33$
$\Rightarrow$ Minimum value of $\mathrm{Z}=112$ at $\mathrm{x}=2, \mathrm{y}=4$ i.e., least value
of mixture is $₹ 112$ when $2 \mathrm{~kg}$ of food $x$ and $4 \mathrm{~kg}$ of food $y$
are mixed.
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.