Search any question & find its solution
Question:
Answered & Verified by Expert
(a) Find the M.I. of a sphere about a tangent to the sphere, given the M.I. of the sphere about any of its diameters to be $\frac{2}{5} M R^2$, where $M$ is the mass and $\mathrm{R}$ is the radius of the sphere.
(b) What is the moment of inertia of a uniform circular disc of radius $R$ and mass $M$ about an axis (i) passing through its centre and normal to the disc, (ii) passing through a point on its edge and normal to the disc? The moment of inertia of the disc about any of its diameters is given to be $\frac{1}{4} M R^2$.
(b) What is the moment of inertia of a uniform circular disc of radius $R$ and mass $M$ about an axis (i) passing through its centre and normal to the disc, (ii) passing through a point on its edge and normal to the disc? The moment of inertia of the disc about any of its diameters is given to be $\frac{1}{4} M R^2$.
Solution:
1585 Upvotes
Verified Answer
(a) Given, $I_{A B}=\frac{2}{5} M R^2, I_{C D}=$ ?
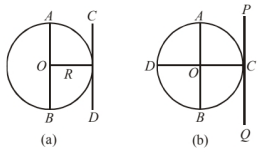
By parallel axes theorem, $I_{C D}=I_{A B}+M R^2$ $\Rightarrow \frac{2}{5} M R^2+M R^2=\frac{7}{5} M R^2$
(b) Consider 2 diameters $A B$ and $C D$ symmetrical to each other
$I_{A B}=I_{C D}=\frac{1}{4} M R^2$ (Given)
(i) By $\perp$ axes theorem, M.I. of the disc about an axis passing through its centre and normal to its plane $I_{X Y}=I_{A B}+I_{C D}=2 \times \frac{1}{4} M R^2=\frac{1}{2} M R^2$
(ii) By parallel axes theorem, M.I of the disc about an axis passing through its edge and $\perp$ to its plane $I_{P Q}=I_{X Y}+M R^2$
$$
=\frac{1}{2} M R^2+M R^2=\frac{3}{2} M R^2
$$

By parallel axes theorem, $I_{C D}=I_{A B}+M R^2$ $\Rightarrow \frac{2}{5} M R^2+M R^2=\frac{7}{5} M R^2$
(b) Consider 2 diameters $A B$ and $C D$ symmetrical to each other
$I_{A B}=I_{C D}=\frac{1}{4} M R^2$ (Given)
(i) By $\perp$ axes theorem, M.I. of the disc about an axis passing through its centre and normal to its plane $I_{X Y}=I_{A B}+I_{C D}=2 \times \frac{1}{4} M R^2=\frac{1}{2} M R^2$
(ii) By parallel axes theorem, M.I of the disc about an axis passing through its edge and $\perp$ to its plane $I_{P Q}=I_{X Y}+M R^2$
$$
=\frac{1}{2} M R^2+M R^2=\frac{3}{2} M R^2
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.