Search any question & find its solution
Question:
Answered & Verified by Expert
A fish rising vertically to the surface of water in a lake uniformly at the rate of $2 \mathrm{~m} / \mathrm{s}$ observes a kingfisher diving vertically towards the water at a rate of $10 \mathrm{~m} / \mathrm{s}$. If refractive index of water $n=\frac{4}{3}$, what will be the actual velocity of the kingfisher
Options:
Solution:
2640 Upvotes
Verified Answer
The correct answer is:
$6 \mathrm{~m} / \mathrm{s}$
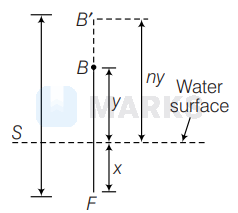
$\because$ Velocity of bird w.r.t. fish,
$v_{B \rightarrow F}=10 \mathrm{~m} / \mathrm{s}$
and velocity of fish w.r.t. ground
$V_{F \rightarrow G}=2 \mathrm{~m} / \mathrm{s}$
$\therefore$ Distance between bird and fish, as seen by fish
$S=x+n y$
on differentiating w.r.t. time, we get
$\begin{aligned} & \frac{d S}{d t}=\frac{d x}{d t}+n \frac{d y}{d t} \\ & v_{B \rightarrow F}=v_{F \rightarrow G}+n \cdot v_{B \rightarrow G} \\ & \Rightarrow \quad 10=2+\frac{4}{3} v_{B \rightarrow G} \\ & \Rightarrow \quad v_{B \rightarrow G}=\frac{8}{4 / 3}=6 \mathrm{~m} / \mathrm{s} \\ & \end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.