Search any question & find its solution
Question:
Answered & Verified by Expert
A graph of potential energy $V(x)$ versus $x$ is shown in figure. A particle of energy $E_0$ is executing motion in it. Draw graph of velocity and kinetic energy versus $x$ for one complete cycle $A F A$.
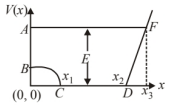

Solution:
2534 Upvotes
Verified Answer
KE versus ( $x$ ) graph : According to the law of conservation of energy.
Total Mechanical energy: $\mathrm{ME}=\mathrm{KE}+\mathrm{PE}$
$$
\begin{aligned}
&E_0=\mathrm{KE}+V(x) \\
&\mathrm{KE}=E_0-V(x) \\
&\text { at } A_1 x=0, V(x)=E_0 \\
&\Rightarrow \mathrm{KE}=E_0-E_0=0
\end{aligned}
$$
At $B_1 V(x) < E_0, \quad x=0, \mathrm{PE}=V_B$ (Let)
So, $\mathrm{KE}=\left(E_0-V_0\right)$
$(\mathrm{KE}>0)$ (Positive)
At $C, X=X_1, \mathrm{PE}=0, \mathrm{KE}=E_0-V(x)=E_0-0=E_0$
At $D, X=X_2, \mathrm{KE}=E_0$
$X=X_3, \mathrm{PE}=E_0$
At $E$, hence $\mathrm{KE}=0$
The variation is shown in figure below.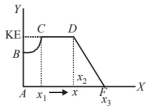
Velocity $(v)$ versus $(x)$ graph.
As $\mathrm{KE}=\frac{1}{2} m v^2$
$\therefore$ At point $A$ and $F$, where $\mathrm{KE}=0, v=0$.
So, $X_A=0, X_D=X_3$.
At point $C$ and $D,\left(X_C=X_1, X_P=X_2\right)$
$\mathrm{KE}$ is maximum, $\left(\mathrm{KE}=E_0\right)$
So, $v$ is $\pm \max , V_{\max }=\pm \sqrt{E_0}=V_0$
At point $B, \mathrm{KE}$ is positive but not maximum.
$$
\mathrm{KE}=E_1
$$
So, $v_B$ is $\pm$ some value
$$
v_B=\sqrt{E_1}=\pm V \quad( < \max )
$$
The graph shows the relation between variation $(X)$.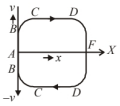
Total Mechanical energy: $\mathrm{ME}=\mathrm{KE}+\mathrm{PE}$
$$
\begin{aligned}
&E_0=\mathrm{KE}+V(x) \\
&\mathrm{KE}=E_0-V(x) \\
&\text { at } A_1 x=0, V(x)=E_0 \\
&\Rightarrow \mathrm{KE}=E_0-E_0=0
\end{aligned}
$$
At $B_1 V(x) < E_0, \quad x=0, \mathrm{PE}=V_B$ (Let)
So, $\mathrm{KE}=\left(E_0-V_0\right)$
$(\mathrm{KE}>0)$ (Positive)
At $C, X=X_1, \mathrm{PE}=0, \mathrm{KE}=E_0-V(x)=E_0-0=E_0$
At $D, X=X_2, \mathrm{KE}=E_0$
$X=X_3, \mathrm{PE}=E_0$
At $E$, hence $\mathrm{KE}=0$
The variation is shown in figure below.

Velocity $(v)$ versus $(x)$ graph.
As $\mathrm{KE}=\frac{1}{2} m v^2$
$\therefore$ At point $A$ and $F$, where $\mathrm{KE}=0, v=0$.
So, $X_A=0, X_D=X_3$.
At point $C$ and $D,\left(X_C=X_1, X_P=X_2\right)$
$\mathrm{KE}$ is maximum, $\left(\mathrm{KE}=E_0\right)$
So, $v$ is $\pm \max , V_{\max }=\pm \sqrt{E_0}=V_0$
At point $B, \mathrm{KE}$ is positive but not maximum.
$$
\mathrm{KE}=E_1
$$
So, $v_B$ is $\pm$ some value
$$
v_B=\sqrt{E_1}=\pm V \quad( < \max )
$$
The graph shows the relation between variation $(X)$.

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.