Search any question & find its solution
Question:
Answered & Verified by Expert
A light bulb of resistance $R=16 \Omega$ is attached in series with an infinite resistor network. with identical resistances $\mathrm{r}$ as shown below. A $10 \mathrm{~V}$ battery derives current in the circuit. What should be the value of $r$ such that the bulb dissipated about $1 \mathrm{~W}$ of power.
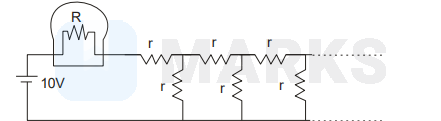
Options:

Solution:
1596 Upvotes
Verified Answer
The correct answer is:
$14.8 \Omega$
$$
\begin{array}{l}
\mathrm{P}_{\text {bulb }}=\frac{v^{2}}{R}=i^{2} R \\
1=\frac{v^{2}}{16} \\
\mathrm{~V}_{\mathrm{B}}=4 \mathrm{~V} \\
1=i^{2} \times 16 \\
\mathrm{I}_{\mathrm{B}}=\frac{1}{4} \mathrm{Amp} . \\
6=\frac{1}{4} \times r_{e q}(\text { equivalent of groups of } \mathrm{r})
\end{array}
$$
Where
$$
r_{e q}=r+\frac{r_{e q} \cdot r}{r_{e q}+r}
$$
\begin{array}{l}
\mathrm{P}_{\text {bulb }}=\frac{v^{2}}{R}=i^{2} R \\
1=\frac{v^{2}}{16} \\
\mathrm{~V}_{\mathrm{B}}=4 \mathrm{~V} \\
1=i^{2} \times 16 \\
\mathrm{I}_{\mathrm{B}}=\frac{1}{4} \mathrm{Amp} . \\
6=\frac{1}{4} \times r_{e q}(\text { equivalent of groups of } \mathrm{r})
\end{array}
$$
Where
$$
r_{e q}=r+\frac{r_{e q} \cdot r}{r_{e q}+r}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.