Search any question & find its solution
Question:
Answered & Verified by Expert
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses $0.36 \mathrm{~kg}$ and $0.72 \mathrm{~kg}$. Taking $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2},$ find the work done $(\mathrm{in}$
joules) by the string on the block of mass $0.36 \mathrm{~kg}$ during the first second after the system is released from rest.
Options:
joules) by the string on the block of mass $0.36 \mathrm{~kg}$ during the first second after the system is released from rest.

Solution:
1338 Upvotes
Verified Answer
The correct answer is:
$8 \mathrm{~J}$
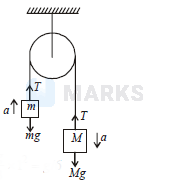
Given $m=0.36 \mathrm{~kg}, M=0.72 \mathrm{~kg}$. The figure shows the forces on $m$ and $M$. When the system is released, let the acceleration be $a$. Then
$T-m g=m a$
$M g-T=M a$
$$
a=\frac{(M-m) g}{M+m}=g / 3
$$
and $T=4 \mathrm{mg} / 3$
For block m:
$$
u=0, a=g / 3, t=1, s=?
$$
$$
s=u t+\frac{1}{2} a t^{2}=0+\frac{1}{2} \times \frac{g}{3} \times 1^{2}=g / 6
$$
Work done by the string on $m$ is
$$
\bar{T} \bar{s}=T s=4 \frac{m g}{3} \times \frac{g}{6}=\frac{4 \times 0.36 \times 10 \times 10}{3 \times 6}=8 \mathrm{~J}
$$
$T-m g=m a$
$M g-T=M a$
$$
a=\frac{(M-m) g}{M+m}=g / 3
$$
and $T=4 \mathrm{mg} / 3$
For block m:
$$
u=0, a=g / 3, t=1, s=?
$$

$$
s=u t+\frac{1}{2} a t^{2}=0+\frac{1}{2} \times \frac{g}{3} \times 1^{2}=g / 6
$$
Work done by the string on $m$ is
$$
\bar{T} \bar{s}=T s=4 \frac{m g}{3} \times \frac{g}{6}=\frac{4 \times 0.36 \times 10 \times 10}{3 \times 6}=8 \mathrm{~J}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.