Search any question & find its solution
Question:
Answered & Verified by Expert
A light ray enters through a right angled prism at point $P$ with the angle of incidence $30^{\circ}$ as shown in figure. It travels through the prism parallel to its base $B C$ and emerges along the face $A C$. The refractive index of the prism is:
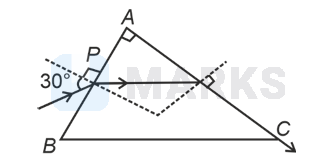
Options:

Solution:
1708 Upvotes
Verified Answer
The correct answer is:
$\frac{\sqrt{5}}{2}$
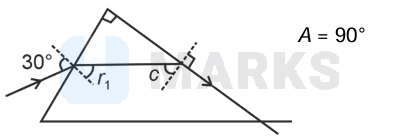
In prism, $r_1+c=A$
$\begin{gathered}
r_1=90^{\circ}-c \ldots(1)\\
\sin c=\frac{1}{\mu} \Rightarrow \cos c=\frac{\sqrt{\mu^2-1}}{\mu}
\end{gathered}$
$\Rightarrow$ Apply Snell's law, on incidence surface
$\begin{aligned}
1 \cdot \sin 30^{\circ}=\mu \sin \left(r_1\right) \Rightarrow 1 \times \frac{1}{2} & =\mu \times \sin \left(90^{\circ}-c\right) \\
\frac{1}{2} & =\mu \times \frac{\sqrt{\mu^2-1}}{\mu}
\end{aligned}$
On squaring $\frac{1}{4}=\mu^2-1$
$\Rightarrow \mu^2=\frac{5}{4} \Rightarrow \mu=\frac{\sqrt{5}}{2}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.