Search any question & find its solution
Question:
Answered & Verified by Expert
A line $L$ makes intercepts $a$ and $b$ on the coordinate axes. The axes are rotated through an angle $\theta$ in the positive direction, keeping the origin fixed. If the line $L$ makes intercepts $p$ and $q$ on the new coordinate axes, then $\frac{1}{a^2}+\frac{1}{b^2}=$
Options:
Solution:
2907 Upvotes
Verified Answer
The correct answer is:
$\frac{1}{p^2}+\frac{1}{q^2}$
$$
\text { Let the equation of line is } \frac{x}{a}+\frac{y}{b}=1 \text {. }
$$
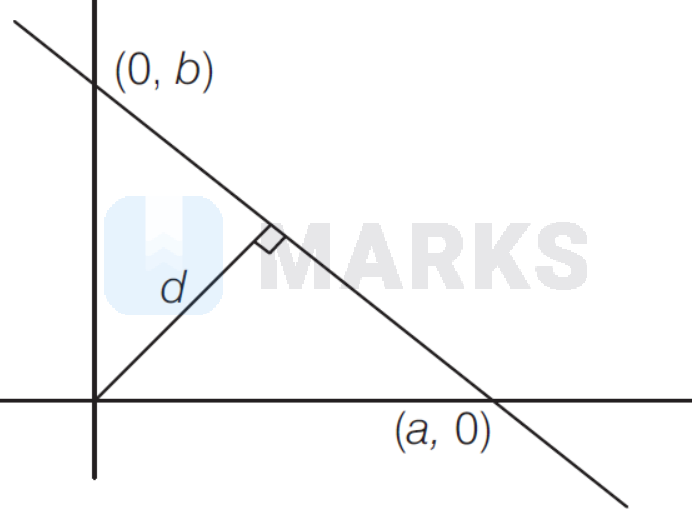
Distance from origin
$$
d=\left|\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}\right| \Rightarrow \frac{1}{d^2}=\frac{1}{a^2}+\frac{1}{b^2}
$$
When line is rotated perpendicular distance from origin is same of line $\frac{x}{p}+\frac{y}{q}=1$
i.e. $d=\left|\frac{1}{\sqrt{\frac{1}{p^2}+\frac{1}{q^2}}}\right| \Rightarrow \frac{1}{d^2}=\frac{1}{p^2}+\frac{1}{q^2}$
From, Eqs. (i) and (ii), we get
$$
\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}+\frac{1}{q^2}
$$
\text { Let the equation of line is } \frac{x}{a}+\frac{y}{b}=1 \text {. }
$$

Distance from origin
$$
d=\left|\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}\right| \Rightarrow \frac{1}{d^2}=\frac{1}{a^2}+\frac{1}{b^2}
$$
When line is rotated perpendicular distance from origin is same of line $\frac{x}{p}+\frac{y}{q}=1$
i.e. $d=\left|\frac{1}{\sqrt{\frac{1}{p^2}+\frac{1}{q^2}}}\right| \Rightarrow \frac{1}{d^2}=\frac{1}{p^2}+\frac{1}{q^2}$
From, Eqs. (i) and (ii), we get
$$
\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}+\frac{1}{q^2}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.