Search any question & find its solution
Question:
Answered & Verified by Expert
A line segment of length moves such that the points and remain on the periphery of a circle of radius . Then the locus of the point, that divides the line segment in the ratio , is a circle of radius
Options:
Solution:
1519 Upvotes
Verified Answer
The correct answer is:
Given,
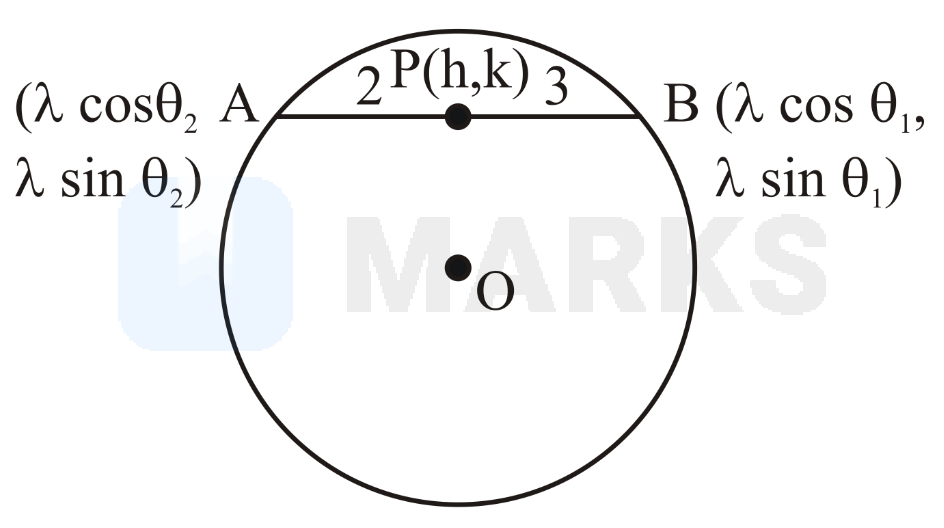
A line segment of length moves such that the points and remain on the periphery of a circle of radius ,
Now taking the points on the circle of radius as and taking the point which divides the line segment in of length in
Now plotting the diagram we get,
Now, let be the origin and radius of circle is and and using distance formula we get,
Now using section formula we get,
and
Now squaring and adding above two value we get,
Hence, Radius
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.